Question

【题目】如图，直线l1的解析表达式为y=- x-1，且l1与x轴交于点D，直线l2经过定点A（2，0），B（-1，3），直线l1与l2交于点C．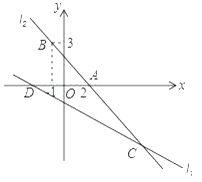

（1）求直线l2的函数关系式；
（2）求△ADC的面积；
（3）在直线l2上存在异于点C的另一点P，使得△ADP与△ADC的面积相等，请写出点P的坐标．

Answer 1

【答案】
（1）解：设l2的函数关系式为：y=kx+b，

∵直线过A（2，0），B（-1，3），

∴ ，解得： ，

∴l2的函数关系式为：y=-x+2

（2）解：∵l1的解析表达式为y=- x-1，

∴D点坐标是（-2，0），

∵直线l1与l2交于点C．

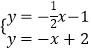∴ ，解得 ，

∴C（6，-4），

△ADC的面积为： ×AD×4= ×4×4=8

（3）解：∵△ADP与△ADC的面积相等，

∴△ADP的面积为8，

∵AD长是4，

∴P点纵坐标是4，

再根据P在l2上，则4=-x+2，解得：x=-2，

故P点坐标为：（-2，4）

【解析】(1)用待定系数法求出直线l2的函数关系式；
（2）先求出D点的坐标，然后解直线l1与l2的解析式组成的方程组，求出C点的坐标，然后利用面积公式计算出△ADC的面积；
（3）根据△ADP与△ADC的面积相等，得出AD的长，从而得出P点纵坐标是4，把P点的纵坐标代入l2得解析式，求出P点的横坐标，从而得出P点的坐标。
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识，掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法．