题目内容
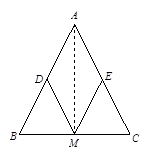
【题目】如图,已知:△ABC中,AB=AC,M、D、E分别是BC、AB、AC的中点.
(1)求证:MD=ME;
(2)若MD=3,求AC的长.
【答案】
(1)证明:连接AM,∵AB=AC,M是BC的中点,∴AM⊥BC.∵在Rt△ABM和Rt△ACM中,∠BMA=∠CMA=90°,D、E分别是AB、AC的中点,∴MD= ![]() AB,ME=
AB,ME= ![]() AC .∵AB=AC,∴MD=ME .
AC .∵AB=AC,∴MD=ME .
(2)解:∵MD=3,
MD= ![]() AB,∴AC=AB=6.
AB,∴AC=AB=6.
【解析】(1)连接AM利用等腰三角形的三线合一得出AM⊥BC,然后利用直角三角形斜边上的中线等于斜边的一半得出结论;
(2)由(1)知MD= ![]() AB又AB=AC,得出结论。
AB又AB=AC,得出结论。
【考点精析】本题主要考查了等腰三角形的性质和直角三角形斜边上的中线的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);直角三角形斜边上的中线等于斜边的一半才能正确解答此题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目