题目内容
【题目】如图，四边形ABCD是⊙O的内接四边形，∠ABC=2∠D，连接OA、OB、OC、AC，OB与AC相交于点E，若∠COB=3∠AOB，OC=2
，则图中阴影部分面积是_____（结果保留π和根号）
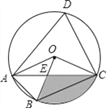
【答案】3π﹣2
【解析】∵四边形ABCD是⊙O的内接四边形，
∴∠ABC+∠D=180°，
∵∠ABC=2∠D，
∴∠D+2∠D=180°，
∴∠D=60°，
∴∠AOC=2∠D=120°，
∵OA=OC，
∴∠OAC=∠OCA=30°；
∵∠COB=3∠AOB，
∴∠AOC=∠AOB+3∠AOB=120°，
∴∠AOB=30°，
∴∠COB=∠AOC﹣∠AOB=90°，
在Rt△OCE中，OC=2
，
∴OE=OCtan∠OCE=2
tan30°=2
×
=2，
∴S△OEC=
OEOC=
×2×2
=2
，
∴S扇形OBC=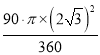
=3π，
∴S阴影=S扇形OBC﹣S△OEC=3π﹣2
．
故答案为：3π﹣2
．
练习册系列答案
相关题目
【题目】为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况，随机抽取了x名学生进行调查统计（要求每名学生选出并且只能选出一个自己最喜爱的节目），并将调查结果绘制成如下统计图表：则 a=___.
学生最喜爱的节目 | 人数（名） | 百分比 |
最强大脑 | 5 | 10% |
朗读者 | 15 | b% |
中国诗词大会 | a | 40% |
出彩中国人 | 10 | 20% |
