题目内容
【题目】甲、乙两车从A地将一批物品匀速运往B地,已知甲出发0.5小时后乙开始出发,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,请结合图中的信息解决如下问题:
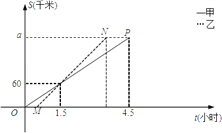
(1)计算甲、乙两车的速度及a的值;
(2)乙车到达B地后以原速立即返回.
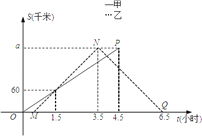
①在图中画出乙车在返回过程中离A地的距离S(km)与时间t(h)的函数图象;
②请问甲车在离B地多远处与返程中的乙车相遇?
【答案】(1)甲车的速度40km/小时,乙车的速度60km/小时,a=180km;(2)①作图见解析;
②甲车在离B地24km处与返程中的乙车相遇.
【解析】解:(1)由题意可知M(0.5,0),线段OP、MN都经过(1.5,60),
甲车的速度60÷1.5=40km/小时,
乙车的速度60÷(1.5﹣0.5)=60km/小时,
a=40×4.5=180km;
(2)①∵180÷60=3小时,∴乙车到达B地,所用时间为180÷60=3,所以点N的横坐标为3.5,
6.5小时返回A地,乙车在返回过程中离A地的距离S(km)与时间t(h)的函数图象为线段NQ;
②甲车离A地的距离是:40×3.5=140km;设乙车返回与甲车相遇所用时间为t0,则(60+40)t0=180﹣140,解得t0=0.4h,60×0.4=24km,答:甲车在离B地24km处与返程中的乙车相遇.

【题目】我市某草莓种植农户喜获丰收,共收获草莓2000kg.经市场调查,可采用批发、零售两种销售方式,这两种销售方式每kg草莓的利润如下表:
销售方式 | 批发 | 零售 |
利润(元/kg) | 6 | 12 |
设按计划全部售出后的总利润为y元,其中批发量为xkg.
(1)求y与x之间的函数关系式;
(2)若零售量不超过批发量的4倍,求该农户按计划全部售完后获得的最大利润.