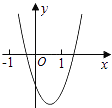题目内容
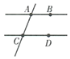
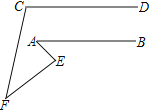
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.
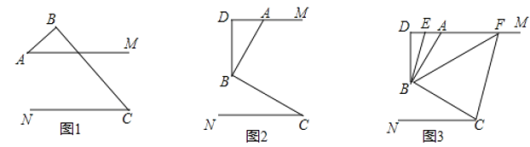
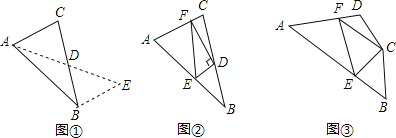
(1)如图1,直接写出∠A和∠C之间的数量关系___;
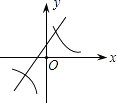
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
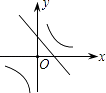
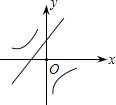
(3)如图3,在(2)问的条件下,点E. F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
【答案】(1)∠A+∠C=90°;(2)见解析;(3)105°.
【解析】
(1)根据平行线的性质以及直角三角形的性质进行解答即可;
(2)先过点B作BG∥DM,根据同角的余角相等,得出∠ABD=∠CBG,再根据平行线的性质,得出∠C=∠CBG,即可得到∠ABD=∠C;
(3)先过点B作BG∥DM,根据角平分线的定义,得出∠ABF=∠GBF,再设∠DBE=α,∠ABF=β,根据∠CBF+∠BFC+∠BCF=180°,可得(2α+β)+3α+(3α+β)=180°,根据AB⊥BC,可得β+β+2α=90°,最后解方程组即可得到∠ABE=15°,进而得出∠EBC=∠ABE+∠ABC=15°+90°=105°.
(1)如图1,∵AM∥CN,
∴∠C=∠AOB,
∵AB⊥BC,
∴∠A+∠AOB=90°,
∴∠A+∠C=90°,
故答案为∠A+∠C=90°;
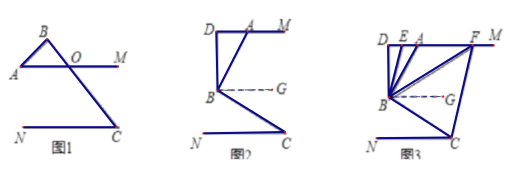
(2)如图2,过点B作BG∥DM,
∵BD⊥AM,
∴DB⊥BG,即∠ABD+∠ABG=90°,
又∵AB⊥BC,
∴∠CBG+∠ABG=90°,
∴∠ABD=∠CBG,
∵AM∥CN∥BG,
∴∠C=∠CBG,
∴∠ABD=∠C;
(3)如图3,过点B作BG∥DM,
∵BF平分∠DBC,BE平分∠ABD,
∴∠DBF=∠CBF,∠DBE=∠ABE,
由(2)可得∠ABD=∠CBG,
∴∠ABF=∠GBF,
设∠DBE=α,∠ABF=β,
则∠ABE=α,∠ABD=2α=∠CBG,∠GBF=β=∠AFB,∠BFC=3∠DBE=3α,
∴∠AFC=3α+β,
∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,
∴∠FCB=∠AFC=3α+β,
在△BCF中,由∠CBF+∠BFC+∠BCF=180°,
可得 (2α+β)+3α+(3α+β)=180°,①
由AB⊥BC,可得
β+β+2α=90°,②
由①②联立方程组,解得α=15°,
∴∠ABE=15°,
∴∠EBC=∠ABE+∠ABC=15°+90°=105°.

 阅读快车系列答案
阅读快车系列答案