题目内容
【题目】(1)阅读理解:

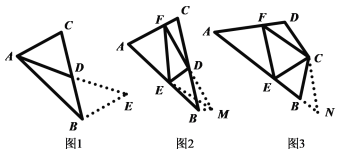
如图①,在△ABC中,若AB=8,AC=4,求BC边上的中线AD的取值范围是
(2)问题解决:如图②,在△ABC中D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70角的两边分别交AB,AD于E,F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.
【答案】(1)2<AD<6;(2)证明见解析;(3)BE+DF=EF,证明见解析
【解析】
(1)如图1(见解析),先根据三角形全等的判定定理与性质得出![]() ,再根据三角形的三边关系定理即可得;
,再根据三角形的三边关系定理即可得;
(2)如图2(见解析),先同(1),根据三角形全等的判定定理与性质得出![]() ,再根据垂直平分线的判定与性质得出
,再根据垂直平分线的判定与性质得出![]() ,然后根据三角形的三边关系定理、等量代换即可得证;
,然后根据三角形的三边关系定理、等量代换即可得证;
(3)如图3(见解析),先根据角的和差得出![]() ,再根据三角形全等的判定定理与性质可得
,再根据三角形全等的判定定理与性质可得![]() ,
,![]() ,从而可得
,从而可得![]() ,然后根据三角形全等的判定定理与性质可得
,然后根据三角形全等的判定定理与性质可得![]() ,最后根据线段的和差、等量代换即可得.
,最后根据线段的和差、等量代换即可得.
(1)如图1,延长AD至E,使![]() ,连接BE
,连接BE
∵AD是BC边上的中线
∴![]()
在![]() 和
和![]() 中,
中,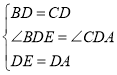
∴![]()
∴![]()
在![]() 中,由三角形的三边关系得:
中,由三角形的三边关系得:![]()
∴![]() ,即
,即![]()
∴![]() ,即
,即![]()
∴![]()
故答案为:![]() ;
;
(2)如图2,延长FD至点M,使![]() ,连接BM、EM
,连接BM、EM
同(1)得:![]()
∴![]()
∵![]() ,
,![]()
∴![]() 是
是![]() 的垂直平分线
的垂直平分线
∴![]()
在![]() 中,由三角形的三边关系得:
中,由三角形的三边关系得:![]()
∴![]() ;
;
(3)![]() ;证明如下:
;证明如下:
如图3,延长AB至点N,使![]() ,连接CN
,连接CN
∵![]() ,
,![]()
∴![]()
在![]() 和
和![]() 中,
中,
∴![]()
∴![]() ,
,![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∴![]()
在![]() 和
和![]() 中,
中,
∴![]()
∴![]()
∵![]()
∴![]() .
.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目