题目内容
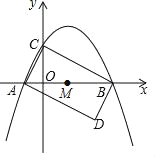
【题目】如图,抛物线y=ax2+bx+2与x轴相交于A(﹣1,0),B(4,0)两点,与y轴相交于点C.
(1)求抛物线的解析式;
(2)将△ABC绕AB中点M旋转180°,得到△BAD.
①求点D的坐标;
②判断四边形ADBC的形状,并说明理由;
(3)在该抛物线对称轴上是否存在点P,使△BMP与△BAD相似?若存在,请求出所有满足条件的P点的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)①点D的坐标为(3,﹣2),②四边形ADBC为矩形,理由见解析;(3)在该抛物线对称轴上存在点P,使△BMP与△BAD相似,点P的坐标为(
x+2;(2)①点D的坐标为(3,﹣2),②四边形ADBC为矩形,理由见解析;(3)在该抛物线对称轴上存在点P,使△BMP与△BAD相似,点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() )或(
)或(![]() ,5)或(
,5)或(![]() ,﹣5).
,﹣5).
【解析】
(1)由点A、B的坐标,利用待定系数法即可求出抛物线的解析式;
(2)利用二次函数图象上点的坐标特征可求出点C的坐标.①过点D作DE⊥x轴于点E,根据旋转的性质可得出OA=EB、OC=ED,结合点A、B、O、C的坐标,即可找出点D的坐标;②由点A、B、C的坐标可得出OA、OC、OB的长度,利用勾股定理可求出AC、BC的长,由AC2+BC2=25=AB2可得出∠ACB=90°,再利用旋转的性质即可找出四边形ADBC为矩形;
(3)假设存在,设点P的坐标为(![]() ,m),由点M为AB的中点可得出∠BPD=∠ADB=90°,分△PMB∽△BDA及△BMP∽△BDA两种情况考虑,利用相似三角形的性质可得出关于m的含绝对值的一元一次方程,解之即可得出结论.
,m),由点M为AB的中点可得出∠BPD=∠ADB=90°,分△PMB∽△BDA及△BMP∽△BDA两种情况考虑,利用相似三角形的性质可得出关于m的含绝对值的一元一次方程,解之即可得出结论.
(1)将A(﹣1,0)、B(4,0)代入y=ax2+bx+2,得:![]() ,解得:
,解得:![]() ,
,
∴抛物线的解析式为y=﹣![]() x2+
x2+![]() x+2.
x+2.
(2)当x=0时,y=﹣![]() x2+
x2+![]() x+2=2,
x+2=2,
∴点C的坐标为(0,2).
①过点D作DE⊥x轴于点E,如图1所示.
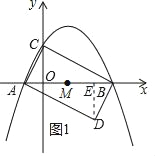
∵将△ABC绕AB中点M旋转180°,得到△BAD,
∴OA=EB,OC=ED.
∵A(﹣1,0),O(0,0),C(0,2),B(4,0),
∴BE=1,DE=2,OE=3,
∴点D的坐标为(3,﹣2).
②四边形ADBC为矩形,理由如下:
∵A(﹣1,0),B(4,0),C(0,2),
∴OA=1,OC=2,OB=4,AB=5,
∴AC=![]() ,BC=
,BC=![]() .
.
∵AC2+BC2=25=AB2,
∴∠ACB=90°.
∵将△ABC绕AB中点M旋转180°,得到△BAD,
∴∠ABC=∠BAD,BC=AD,
∴BC∥AD且BC=AD,
∴四边形ADBC为平行四边形.
又∵∠ACB=90°,
∴四边形ADBC为矩形.
(3)假设存在,设点P的坐标为(![]() ,m).
,m).
∵点M为AB的中点,
∴∠BPD=∠ADB=90°,
∴有两种情况(如图2所示).
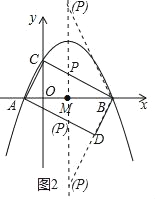
①当△PMB∽△BDA时,有![]() ,即
,即![]() ,
,
解得:m=±![]() ,
,
∴点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() );
);
②当△BMP∽△BDA时,有![]() ,即
,即![]() ,
,
解得:m=±5,
∴点P的坐标为(![]() ,5)或(
,5)或(![]() ,﹣5).
,﹣5).
综上所述:在该抛物线对称轴上存在点P,使△BMP与△BAD相似,点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() )或(
)或(![]() ,5)或(
,5)或(![]() ,﹣5).
,﹣5).

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案【题目】![]() 朗读者
朗读者![]() 自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级
自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级![]() 、
、![]() 班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩
班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩![]() 满分为100分
满分为100分![]() 如图所示.
如图所示.
平均数 | 中位数 | 众数 | |
九 | 85 | 85 | |
九 | 80 |
![]() 根据图示填写表格;
根据图示填写表格;
![]() 结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
![]() 如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.