��Ŀ����
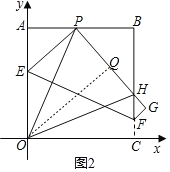
����Ŀ����ͼ����һ�ű߳�Ϊ8��������ֽƬOABC����ֱ������ϵ�У�ʹ��OA��y���غϣ�OC��x���غϣ���PΪ������AB���ϵ�һ��(�����A����B�غ�)����������ֽƬ�۵���ʹ��O����P������C����G����PG��BC��H���ۺ�ΪEF������OP��OH��
����̽��
��1����AP=4ʱ
��ֱ��д����E����������������
����ֱ��EF�ĺ�������ʽ��
����̽��
��2������P�ڱ�AB���ƶ�ʱ����APO���OPH�Ķ���������ȣ���˵�����ɣ�
��չӦ��
��3������P�ڱ�AB���ƶ�ʱ����PBH���ܳ��Ƿ����仯����֤����Ľ��ۣ�
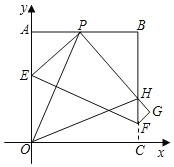
���𰸡���1����(0��5)����![]() ����2�����ɼ���������3���ܳ�=16�����ᷢ���仯��֤����������
����2�����ɼ���������3���ܳ�=16�����ᷢ���仯��֤����������
��������
��1�����裺OE��PE��a����AE��8��a��AP��4����Rt��AEP�У��ɹ��ɶ����ã�PE2��AE2+AP2��������⣻
��֤����AOP�ա�FRE��AAS������ER��AP��4���ʵ�F��8��1����������⣻
��2����EOP����EPO������EPH����EOC��90�����ʡ�EPH����EPO����EOC����EOP������POC����OPH������ΪAB��OC���ʡ�APO����POC��������⣻
��3��֤����AOP�ա�QOP��AAS������OCH�ա�OQH��SAS������CH��QH��������⣮
��1�����裺OE=PE=a����AE=8��a��AP=4��
��Rt��AEP�У��ɹ��ɶ����ã�PE2=AE2+AP2��
��a2=(8��a)2+16����ã�a=5��
�ʵ�E(0��5)��
�ʴ�Ϊ��(0��5)��
������F��FR��y���ڵ�R��
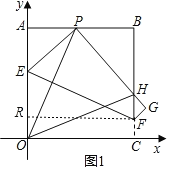
�۵����O����P�������O��P����ֱ��EF�Գƣ���OP��EF��
���EFR+��FER=90��������FER+��AOP=90����
���AOP=��EFR��
����OAP=��FRE��RF=AO��
���AOP�ա�FRE(AAS)��
��ER=AP=4��
OR=EO��OR=5��4=1���ʵ�F(8��1)��
����E��F���������һ�κ�������ʽ��y=kx+b
�ã�![]() ����ã�
����ã�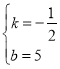 ��
��
��ֱ��EF�ı���ʽΪ��y=��![]() x+5��
x+5��
��2����PE=OE��
���EOP=��EPO��
���ߡ�EPH=��EOC=90����
���EPH����EPO=��EOC����EOP��
����POC=��OPH��
����AB��OC��
���APO=��POC��
���APO=��OPH��
��3����ͼ����O��OQ��PH������ΪQ��
�ɣ�1��֪��APO=��OPH��
����AOP����QOP��
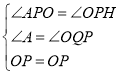
���AOP�ա�QOP(AAS)��
��AP=QP��AO=OQ��
����AO=OC��
��OC=OQ��
���ߡ�C=��OQH=90����OH=OH��
���OCH�ա�OQH(SAS)��
��CH=QH��
���PHB���ܳ�=PB+BH+PH=AP+PB+BH+HC=AB+CB=16��
�ʴ�Ϊ��16��

 ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�