题目内容
若抛物线y=x2+bx+c与x轴只有一个交点,且过点A(m,n),B(m+6,n),则n= .
9
分析:∵抛物线y=x2+bx+cx轴只有一个交点,∴当
 时,y=0.且b2﹣4c=0,即b2=4c.
时,y=0.且b2﹣4c=0,即b2=4c.又∵点A(m,n),B(m+6,n),∴点A、B关于直线
 对称。
对称。∴A(
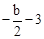 ,n),B(
,n),B( ,n)。
,n)。将A点坐标代入抛物线解析式,得:
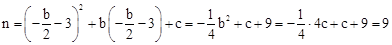 。
。
练习册系列答案
相关题目
题目内容
 时,y=0.且b2﹣4c=0,即b2=4c.
时,y=0.且b2﹣4c=0,即b2=4c. 对称。
对称。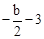 ,n),B(
,n),B( ,n)。
,n)。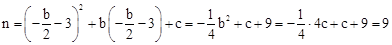 。
。