题目内容
如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线 经过点A、B、C.
经过点A、B、C.

(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其坐标为t,
①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时,点P的坐标;
②是否存在一点P,使△PCD得面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.
 经过点A、B、C.
经过点A、B、C.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其坐标为t,
①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时,点P的坐标;
②是否存在一点P,使△PCD得面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.
(1)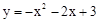
(2)①P点的坐标为:(﹣1,4)或(﹣2,3)。
②当t=﹣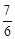 时,S△PCD的最大值为
时,S△PCD的最大值为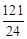 。
。
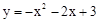
(2)①P点的坐标为:(﹣1,4)或(﹣2,3)。
②当t=﹣
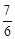 时,S△PCD的最大值为
时,S△PCD的最大值为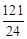 。
。分析:(1)先求出A、B、C的坐标,再运用待定系数法就可以直接求出二次函数的解析式。
(2)①由(1)的解析式可以求出抛物线的对称轴,分类讨论当∠CEF=90°时,当∠CFE=90°时,根据相似三角形的性质就可以求出P点的坐标。
②先运用待定系数法求出直线CD的解析式,设PM与CD的交点为N,根据CD的解析式表示出点N的坐标,再根据S△PCD=S△PCN+S△PDN就可以表示出三角形PCD的面积,运用顶点式就可以求出结论。
解:(1)在Rt△AOB中,OA=1,
 ,∴OB=3OA=3.。
,∴OB=3OA=3.。∵△DOC是由△AOB绕点O逆时针旋转90°而得到的,
∴△DOC≌△AOB。∴OC=OB=3,OD=OA=1。
∴A、B、C的坐标分别为(1,0),(0,3)(﹣3,0).
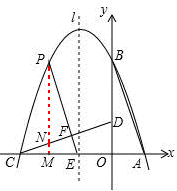
代入解析式得
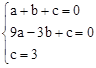 ,解得:
,解得: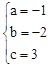 。
。∴抛物线的解析式为
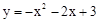 。
。(2)①∵
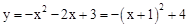 ,∴对称轴l为x=﹣1。
,∴对称轴l为x=﹣1。∴E点的坐标为(﹣1,0)。
当∠CEF=90°时,△CEF∽△COD.此时点P在对称轴上,即点P为抛物线的顶点,P(﹣1,4)。
当∠CFE=90°时,△CFE∽△COD,过点P作PM⊥x轴于点M,则△EFC∽△EMP。
∴
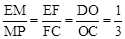 。∴MP=3EM.。
。∴MP=3EM.。∵P的横坐标为t,∴P(t,
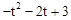 )。
)。∵P在二象限,∴PM=
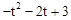 ,EM=
,EM=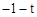 ,
,∴
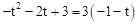 ,解得:t1=﹣2,t2=﹣3(与C重合,舍去)。
,解得:t1=﹣2,t2=﹣3(与C重合,舍去)。∴t=﹣2时,
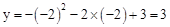 。
。∴P(﹣2,3)。
综上所述,当△CEF与△COD相似时,P点的坐标为:(﹣1,4)或(﹣2,3)。
②设直线CD的解析式为y=kx+b,由题意,得
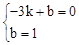 ,解得:
,解得: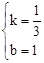 。
。∴直线CD的解析式为:y=
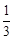 x+1。
x+1。设PM与CD的交点为N,则点N的坐标为(t,
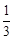 t+1),∴NM=
t+1),∴NM=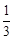 t+1。
t+1。∴
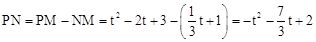 。
。∵S△PCD=S△PCN+S△PDN,
∴
 。
。∴当t=﹣
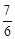 时,S△PCD的最大值为
时,S△PCD的最大值为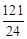 。
。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
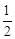 .
.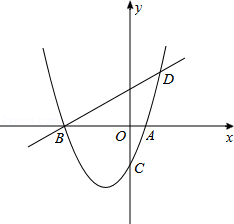
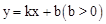 与抛物线
与抛物线 相交于A
相交于A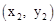 两点,与x轴正半轴相交于点D,与y轴相交于点C,设△OCD的面积为S,且
两点,与x轴正半轴相交于点D,与y轴相交于点C,设△OCD的面积为S,且 。
。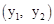 在反比例函数
在反比例函数 的图象上;
的图象上;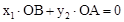 。
。
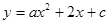 的图象经过点(-2,-5)、(1,4).
的图象经过点(-2,-5)、(1,4).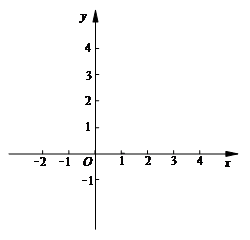
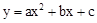 的顶点A(2,0),与y轴的交点为B(0,-1).
的顶点A(2,0),与y轴的交点为B(0,-1).
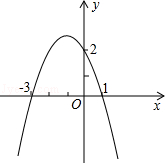
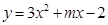 .
. 
 为任何实数,抛物线与x轴总有两个交点;
为任何实数,抛物线与x轴总有两个交点; 的两个有理数根都在
的两个有理数根都在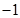 与
与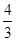 之间(不包括-1、
之间(不包括-1、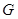 ,再将图象
,再将图象 个单位,若图象
个单位,若图象