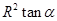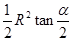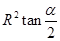题目内容
如图，点A、B、P在⊙O上，且∠APB=50°。若点M是⊙O上的动点，要使△ABM为等腰三角形，则所有符合条件的点M有 ( )
A．1个 B．2个 C．3个 D．4个
A．1个 B．2个 C．3个 D．4个
D
试题分析：分类推论：当MA=MB，则M为AB的垂直平分与圆的两交点，这时两个等腰三角形的顶角分别为50°，130°；当AM=AB，以A为圆心，AB为半径交⊙O于M，此时等腰三角形只有一个，且底角为50°；同理当BM=BA，满足条件的等腰三角形也只有一个．
△ABM为等腰三角形，
当MA=MB，则M为AB的垂直平分与圆的两交点，
这时两个等腰三角形的顶角分别为50°，130°，如图；
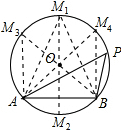
当AM=AB，以A为圆心，AB为半径交⊙O于M，
此时等腰三角形只有一个，且底角为50°；
同理当BM=BA，满足条件的等腰三角形也只有一个，如图，
所以满足条件的等腰三角形有4个．
故选D，
点评：圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，一条弧所对的圆周角是它所对的圆心角的一半．
练习册系列答案
相关题目
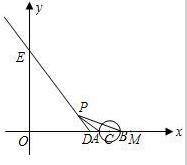
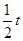个单位长度为半径的⊙C与x轴交于A、B两点（点A在点B的左侧），连接PA、PB．
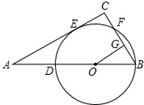
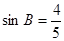，求线段AD的长．
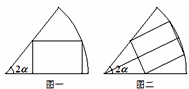
cm2，则这个圆锥的高为 cm.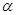
（定值），半径为R（定值），分别在图一、二中作扇形的内接矩形，若按图一作出的矩形面积的最大值为
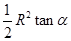，则按图二作出的矩形面积的最大值为（ ）
