题目内容
如图,已知射线DE与x轴和y轴分别交于点D(3,0)和点E(0,4).动点C从点M(5,0)出发,以1个单位长度/秒的速度沿x轴向左作匀速运动,与此同时,动点P从点D出发,也以1个单位长度/秒的速度沿射线DE的方向作匀速运动,设运动时间为t秒,

(1)请用含t的代数式分别表示出点C与点P的坐标;
(2)以点C为中心, 个单位长度为半径的⊙C与x轴交于A、B两点(点A在点B的左侧),连接PA、PB.
个单位长度为半径的⊙C与x轴交于A、B两点(点A在点B的左侧),连接PA、PB.
①当⊙C与射线DE有公共点时,求t的取值范围;
②当△PAB为等腰三角形时,求t的值.

(1)请用含t的代数式分别表示出点C与点P的坐标;
(2)以点C为中心,
 个单位长度为半径的⊙C与x轴交于A、B两点(点A在点B的左侧),连接PA、PB.
个单位长度为半径的⊙C与x轴交于A、B两点(点A在点B的左侧),连接PA、PB.①当⊙C与射线DE有公共点时,求t的取值范围;
②当△PAB为等腰三角形时,求t的值.
(1) 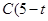 ,
, ,
,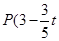 ,
,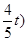 (2)当⊙C与射线DE有公共点时,t的取值范围
(2)当⊙C与射线DE有公共点时,t的取值范围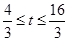
当△PAB为等腰三角形时,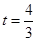 或
或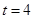 或
或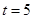 或
或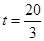
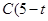 ,
, ,
,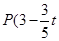 ,
,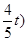 (2)当⊙C与射线DE有公共点时,t的取值范围
(2)当⊙C与射线DE有公共点时,t的取值范围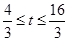
当△PAB为等腰三角形时,
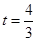 或
或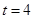 或
或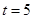 或
或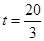
试题分析:解:(1)
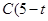 ,
, ,
,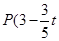 ,
,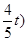
(2)由题意,得点
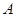 的坐标为
的坐标为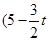 ,
, ,点
,点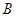 的坐标为
的坐标为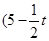 ,
, ,
,①当⊙C的圆心C由(5,0)向左运动,使点A到点D(开始有公共点)并继续向左运动时有
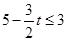 ,即
,即 .
.当点C在点D的左侧时,过点C作CF⊥射线DE于F,
|
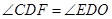 得△CDF∽△EDO,则
得△CDF∽△EDO,则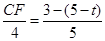 ,解得
,解得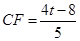 .再由
.再由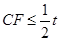 ,即
,即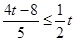 ,解得
,解得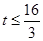 .
.∴当⊙C与射线DE有公共点时,t的取值范围
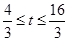 .
.②当PA=AB时,过点P作
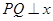 轴,垂足为点Q,
轴,垂足为点Q,有
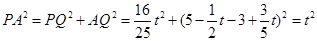 .
.∴
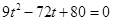 .解得
.解得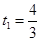 ,
,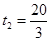 .
.当PA=PB时,有PC⊥AB,∴
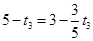 ,解得
,解得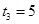 .
.当PB="AB=" t时,有
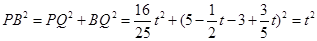 ,
,∴
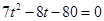 .解得
.解得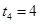 ,
,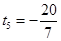 (不合题意,舍去).
(不合题意,舍去).∴当△PAB为等腰三角形时,
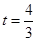 或
或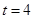 或
或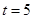 或
或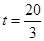
点评:本题难度较大,动点问题是中考题型中非常常见的一类题型,这类题通常都需要学生结合条件总结出运动轨迹所在函数式。注意数形结合思想的运用。

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
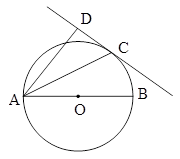
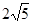 ,CD=2,求⊙O的直径。
,CD=2,求⊙O的直径。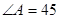 °,则
°,则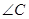 的度数
的度数 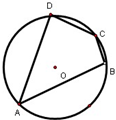

 、
、 轴的正半轴于A、B两点,点P的坐标为(2,0),动点Q从点B处出发,沿圆周按顺时针方向匀速运动一周,设运动的时间为秒.
轴的正半轴于A、B两点,点P的坐标为(2,0),动点Q从点B处出发,沿圆周按顺时针方向匀速运动一周,设运动的时间为秒.
 时,直线PQ恰好与⊙O第一次相切,连接OQ.求此时点Q的运动速度(结果保留
时,直线PQ恰好与⊙O第一次相切,连接OQ.求此时点Q的运动速度(结果保留 );
);