Question

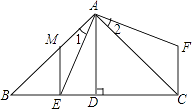
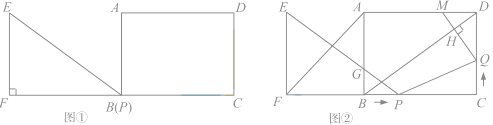
【题目】 已知：Rt△EFP和矩形ABCD如图①摆放（点P与点B重合），点F，B（P），C在同一条直线上，AB＝EF＝6cm，BC＝FP＝8cm，∠EFP＝90°。如图②，△EFP从图①的位置出发，沿BC方向匀速运动，速度为1cm/s；EP与AB交于点G．同时，点Q从点C出发，沿CD方向匀速运动，速度为1cm/s。过Q作QM⊥BD，垂足为H，交AD于M，连接AF，PQ，当点Q停止运动时，△EFP也停止运动．设运动时间为t（s）（0＜t＜6），解答下列问题：

（1）当 t 为何值时，PQ∥BD？

（2）设五边形 AFPQM 的面积为 y（cm2），求 y 与 t 之间的函数关系式；

（3）在运动过程中，是否存在某一时刻 t，使？若存在，求出 t 的值；若不存在，请说明理由；

（4）在运动过程中，是否存在某一时刻 t，使点M在PG的垂直平分线上？若存在，求出 t 的值；若不存在，请说明理由．

Answer 1

【答案】（1）t= ；（2） （3）t=2，9:8（4）t=

【解析】

试题分析：（1）利用△CPQ∽△CBD，列比例式求出t的值；

（2）利用△MDQ∽△CBD，得MD=（6-t），再利用，可求得函数的解析式；

（3）利用=9:8得方程求解；

（4）利用△PBG∽△PEF，得AG、AM，作MN⊥BC，构造矩形MNCD，则MN=6，PN=（8-t）-（6-t）=，然后根据AG2+AN2=PN2+MN2可列方程求解.

试题解析：（1）若PQ∥BD，则△CPQ∽△CBD，可得，即，解得t=；

（2）由∠MQD+∠CDB=∠CBD+∠CDB=90°，可得∠MQD=∠CBD，

又∠MDQ=∠C=90°，∴△MDQ∽△CBD ，

∴

即

解得MD=（6-t），

所以

=

=

即

（3）假使存在t，使

则，即

整理得，解得

答：当t=2，

（4）易证△PBG∽△PEF，

∴，即，∴

则

作MN⊥BC于N点，则四边形MNCD为矩形

所以MN=CD=6，CN=，故：PN=

若M在PG的垂直平分线上，则GM=PM，

所以，所以

即：

整理得：，解得。