题目内容
【题目】如图所示，在菱形ABCD中，AB=4，∠BAD=120°，△AEF为正三角形，点E、F分别在菱形的边BC、CD上滑动，且E、F不与B、C、D重合．
（1）证明不论E、F在BC．CD上如何滑动，总有BE=CF；
（2）当点E、F在BC．CD上滑动时，分别探讨四边形AECF的面积和△CEF的周长是否发生变化？如果不变，求出这个定值；如果变化，求出最小值．
【答案】
（1）证明：如图，连接AC
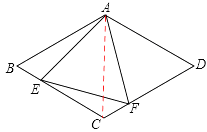
∵四边形ABCD为菱形，∠BAD=120°，
∠BAE+∠EAC=60°，∠FAC+∠EAC=60°，
∴∠BAE=∠FAC
∵∠BAD=120°，
∴∠ABC=60°．
∴△ABC和△ACD为等边三角形
∴∠ACF=60°，AC=AB
∴∠ABE=∠ACF
∴在△ABE和△ACF中，
∵∠BAE=∠FAC，AB=AC，∠ABE=∠ACF，
∴△ABE≌△ACF（ASA）
∴BE=CF
（2）解：四边形AECF的面积不变，△CEF的周长发生变化．理由如下：
由（1）得△ABE≌△ACF，则 
．
∴ 
，是定值
作AH⊥BC于H点，则BH=2，
．
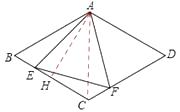
△CEF的周长=CE+CF+EF=CE+BE+EF=BC+EF=BC+AE
由“垂线段最短”可知：当正三角形AEF的边AE与BC垂直时，边AE最短．
故△AEF的周长会随着AE的变化而变化，且当AE最短时，△CEF的周长会最小=4+ 
，
【解析】 （1）连接AC，根据菱形的对角线平分一组对角知：∠BAE+∠EAC=60°，∠FAC+∠EAC=60°，从而得出∠BAE=∠FAC，根据菱形四边相等及对角相等得出△ABC和△ACD为等边三角形，根据等边三角形的性质得出∠ACF=60°，AC=AB，然后由ASA判断出△ABE≌△ACF，根据全等三角形对应边相等得出BE=CF；
（2）四边形AECF的面积不变，△CEF的周长发生变化．理由如下：根据全等三角形的面积相等得出 S Δ A B E = S Δ A C F ，故S 四 边 形 A E C F = S Δ A E C + S Δ A C F = S Δ A E C + S Δ A B E = S Δ A B C ，是定值；作AH⊥BC于H点，则BH=2，△CEF的周长=CE+CF+EF=CE+BE+EF=BC+EF=BC+AE，由“垂线段最短”可知：当正三角形AEF的边AE与BC垂直时，边AE最短．故△AEF的周长会随着AE的变化而变化，且当AE最短时，△CEF的周长会最小。
【考点精析】本题主要考查了垂线段最短和菱形的性质的相关知识点，需要掌握连接直线外一点与直线上各点的所有线段中，垂线段最短；现实生活中开沟引水，牵牛喝水都是“垂线段最短”性质的应用；菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半才能正确解答此题．
