Question

【题目】如图，正三角形的边长为．

如图①，正方形的顶点、在边上，顶点在边上，在正三角形及其内部，以点为位似中心，作正方形的位似正方形，且使正方形的面积最大（不要求写作法）；

求中作出的正方形的边长；

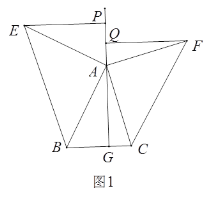
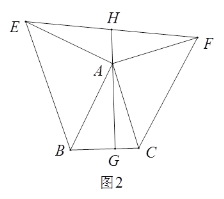
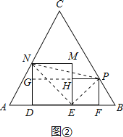
如图②，在正三角形中放入正方形和正方形，使得、在边上，点、分别在边、上，求这两个正方形面积和的最大值和最小值，并说明理由.

Answer 1

【答案】(1)见解析;(2);(3)见解析.

【解析】

（1）如答图①利用位似图形的性质，作出正方形EFPN的位似正方形E′F′P′N′，即为所求.（2）设正方形的边长为，根据正三角形、正方形、直角三角形相关线段之间的关系，利用等式E′F′+AE′+BF′=AB，列方程求得正方形E′F′P′N′的边长即可.（3）设正方形DEMN、正方形EFPH的边长分别为m、n（m≥n），求得面积和的表达式S= ，①当m=n时，S取得最小值；

②当m最大而n最小时，S取得最大值．结合第（1）（2）问m最大n最小的情形即可求得S的最大值.

如图①，正方形即为所求．

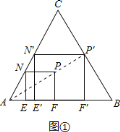
设正方形的边长为，

∵△ABC为正三角形，

∴

∵ ，

∴，

∴，即，（也正确）

如图②，连接、、，则．

设正方形、正方形的边长分别为、，

它们的面积和为，则，．

∴．

∴，

延长交于点，则，

在中，，

∵，即，化简得，

∴，

①当时，即时，最小，

∴，

②当最大时，最大，

即当最大且最小时，最大，

∵，

由知，，

∴，

，（也正确）

综上所述，，；