题目内容
 如图,已知菱形ABCD,AE⊥BC于E,AF⊥CD于F.
如图,已知菱形ABCD,AE⊥BC于E,AF⊥CD于F.(1)求证:CE=CF;
(2)若菱形边长为8,E是BC的中点,求菱形的面积.
分析:(1)由于四边形ABCD是菱形,那么可知AC是∠BCD的角平分线,结合AE⊥BC,AF⊥CD,易得AE=AF,而AC是公共边,易证Rt△AEC≌Rt△AFC,从而有CE=CF;
(2)由于AE⊥BC,E是BC中点,可求BE=4,利用勾股定理易求AE,进而可求△ABC的面积,从而可求菱形ABCD的面积.
(2)由于AE⊥BC,E是BC中点,可求BE=4,利用勾股定理易求AE,进而可求△ABC的面积,从而可求菱形ABCD的面积.
解答: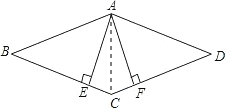 解:如右图所示,连接AC,
解:如右图所示,连接AC,
(1)∵四边形ABCD是菱形,
∴AC是∠BCD的角平分线,
又∵AE⊥BC,AF⊥CD,
∴AE=AF,
又∵AC=AC,
∴Rt△AEC≌Rt△AFC,
∴CE=CF;
(2)∵E是BC中点,AB=BC=8,
∴BE=CE=4,
∴AE=
=4
,
∴S△ABC=
BC×AE=16
,
∴S菱形ABCD=2S△ABC=32
.
 解:如右图所示,连接AC,
解:如右图所示,连接AC,(1)∵四边形ABCD是菱形,
∴AC是∠BCD的角平分线,
又∵AE⊥BC,AF⊥CD,
∴AE=AF,
又∵AC=AC,
∴Rt△AEC≌Rt△AFC,
∴CE=CF;
(2)∵E是BC中点,AB=BC=8,
∴BE=CE=4,
∴AE=
| AB2-BE2 |
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 3 |
∴S菱形ABCD=2S△ABC=32
| 3 |
点评:本题考查了菱形的性质、角平分线性质、全等三角形的判定和性质、勾股定理.解题的关键是连接AC,并求出AE.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
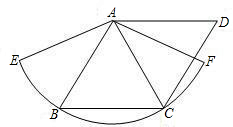 如图,已知菱形ABCD的边长为1.5cm,B,C两点在扇形AEF的
如图,已知菱形ABCD的边长为1.5cm,B,C两点在扇形AEF的
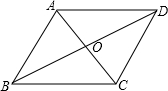 如图,已知菱形ABCD的周长为16cm,∠ABC=60°,对角线AC和BD相交于点O,求AC和BD的长.
如图,已知菱形ABCD的周长为16cm,∠ABC=60°,对角线AC和BD相交于点O,求AC和BD的长.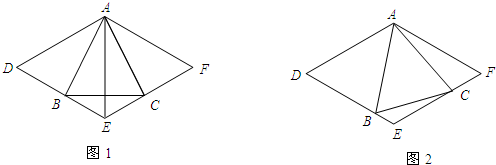
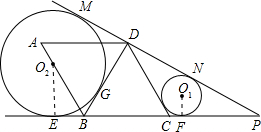 上,半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N,半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G.
上,半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N,半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G.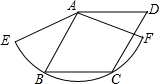 如图,已知菱形ABCD为2cm.B、C两点在以点A为圆心的
如图,已知菱形ABCD为2cm.B、C两点在以点A为圆心的