题目内容
如图,已知菱形ABCD边长为6
,∠ABC=120°,点P在线段BC延长线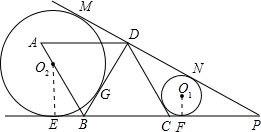 上,半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N,半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G.
上,半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N,半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G.
(1)求菱形的面积;
(2)求证:EF=MN;
(3)求r1+r2的值.
| 3 |
 上,半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N,半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G.
上,半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N,半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G.(1)求菱形的面积;
(2)求证:EF=MN;
(3)求r1+r2的值.
分析:(1)由于菱形ABCD边长为6
,∠ABC=120°,根据菱形的性质得到ADC和△DBC都是等边三角形,利用等边三角形的面积等于边长平方的
倍即可得到菱形的面积=2S△DBC=2×
×(6
)2=54
;
(2)由于PM与PE都是⊙O1的切线,PN与PF都是⊙O2的切线,根据切线长定理得到PM=PN,PN=PE,则PM-PN=PE-PB,即EF=MN;
(3)由于BE与BG都是⊙O1的切线,根据切线的性质和切线长定理得到BE=BG,∠O2BE=∠O2BG,O2E⊥BE,而∠EBG=180°-∠DBC=180°-60°=120°,于是有∠O2BE=60°,∠EO2B=30°,根据含30°的直角三角形三边的关系得到BE=
O2E=
r2,则BG=
r2,DM=DG=6
-
r2,同理可得CF=
r1,DN=DH=6
-
r1,则MN=DM+DN=12
-
(r1+r2),而EF=EB+BC+CF=
r2+6
+
r1=6
+
(r1+r2),利用EF=MN可得到关于(r1+r2)的方程,解方程即可.
| 3 |
| ||
| 4 |
| ||
| 4 |
| 3 |
| 3 |
(2)由于PM与PE都是⊙O1的切线,PN与PF都是⊙O2的切线,根据切线长定理得到PM=PN,PN=PE,则PM-PN=PE-PB,即EF=MN;
(3)由于BE与BG都是⊙O1的切线,根据切线的性质和切线长定理得到BE=BG,∠O2BE=∠O2BG,O2E⊥BE,而∠EBG=180°-∠DBC=180°-60°=120°,于是有∠O2BE=60°,∠EO2B=30°,根据含30°的直角三角形三边的关系得到BE=
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| 3 |
| ||
| 3 |
| ||
| 3 |
| 3 |
| ||
| 3 |
| 3 |
| ||
| 3 |
| ||
| 3 |
| 3 |
| ||
| 3 |
| 3 |
| ||
| 3 |
解答:(1)解:∵菱形ABCD边长为6
,∠ABC=120°,
∴△ADC和△DBC都是等边三角形,
∴菱形的面积=2S△DBC=2×
×(6
)2=54
;
(2)证明:∵PM与PE都是⊙O2的切线,
∴PM=PE,
又∵PN与PF都是⊙O1的切线,
∴PN=PF,
∴PM-PN=PE-PB,即EF=MN;
(3)解:∵BE与BG都是⊙O2的切线,
∴BE=BG,∠O2BE=∠O2BG,O2E⊥BE,
而∠EBG=180°-∠DBC=180°-60°=120°,
∴∠O2BE=60°,∠EO2B=30°,
∴BE=
O2E=
r2,
∴BG=
r2,
∴DM=DG=6
-
r2,
同理可得CF=
r1,DN=DH=6
-
r1,
∴MN=DM+DN=12
-
(r1+r2),
∵EF=EB+BC+CF=
r2+6
+
r1=6
+
(r1+r2),
而EF=MN,
∴6
+
(r1+r2)=12
-
(r1+r2),
∴r1+r2=9.
| 3 |

∴△ADC和△DBC都是等边三角形,
∴菱形的面积=2S△DBC=2×
| ||
| 4 |
| 3 |
| 3 |
(2)证明:∵PM与PE都是⊙O2的切线,
∴PM=PE,
又∵PN与PF都是⊙O1的切线,
∴PN=PF,
∴PM-PN=PE-PB,即EF=MN;
(3)解:∵BE与BG都是⊙O2的切线,
∴BE=BG,∠O2BE=∠O2BG,O2E⊥BE,
而∠EBG=180°-∠DBC=180°-60°=120°,
∴∠O2BE=60°,∠EO2B=30°,
∴BE=
| ||
| 3 |
| ||
| 3 |
∴BG=
| ||
| 3 |
∴DM=DG=6
| 3 |
| ||
| 3 |
同理可得CF=
| ||
| 3 |
| 3 |
| ||
| 3 |
∴MN=DM+DN=12
| 3 |
| ||
| 3 |
∵EF=EB+BC+CF=
| ||
| 3 |
| 3 |
| ||
| 3 |
| 3 |
| ||
| 3 |
而EF=MN,
∴6
| 3 |
| ||
| 3 |
| 3 |
| ||
| 3 |
∴r1+r2=9.
点评:本题考查了圆的综合题:圆的切线垂直于过切点的半径;从圆外一点引圆的两条切线,切线长相等,并且这个点与圆心的连线平分两切线的夹角;掌握菱形的性质,记住等边三角形的面积等于边长平方的
倍以及含30°的直角三角形三边的关系.
| ||
| 4 |

练习册系列答案
相关题目
 如图,已知菱形ABCD的边长为1.5cm,B,C两点在扇形AEF的
如图,已知菱形ABCD的边长为1.5cm,B,C两点在扇形AEF的
 如图,已知菱形ABCD的周长为16cm,∠ABC=60°,对角线AC和BD相交于点O,求AC和BD的长.
如图,已知菱形ABCD的周长为16cm,∠ABC=60°,对角线AC和BD相交于点O,求AC和BD的长.
 如图,已知菱形ABCD为2cm.B、C两点在以点A为圆心的
如图,已知菱形ABCD为2cm.B、C两点在以点A为圆心的