题目内容
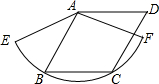 如图,已知菱形ABCD为2cm.B、C两点在以点A为圆心的
如图,已知菱形ABCD为2cm.B、C两点在以点A为圆心的 |
| EF |
 |
| BC |
分析:根据菱形ABCD的边长为2cm,求出AB=BC=2m,再根据AB=AC求得△ABC是等边三角形,进而求得∠BAC=60°,最后根据弧长的计算公式和扇形的面积公式即可求出答案.
解答:解:∵菱形ABCD的边长为2cm,
∴AB=BC=2m,
又∵B、C两点在扇形AEF的
上,
∴AB=BC=AC=2cm,
∴△ABC是等边三角形,
∴∠BAC=60°,
∴
的长l=
=
π(cm),
∴S扇形ABC=
lR=
×
π×2=
π(cm2).
答:
的长为
πcm,扇形ABC的面积是
πcm2.
∴AB=BC=2m,
又∵B、C两点在扇形AEF的
 |
| EF |
∴AB=BC=AC=2cm,
∴△ABC是等边三角形,
∴∠BAC=60°,
∴
 |
| BC |
| 60π×2 |
| 180 |
| 2 |
| 3 |
∴S扇形ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
答:
 |
| BC |
| 2 |
| 3 |
| 2 |
| 3 |
点评:此题考查了扇形面积的计算,用得到的知识点是菱形的性质,等边三角形的性质,关键是求出扇形的半径和圆心角.

练习册系列答案
相关题目
 如图,已知菱形ABCD的边长为1.5cm,B,C两点在扇形AEF的
如图,已知菱形ABCD的边长为1.5cm,B,C两点在扇形AEF的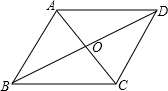 如图,已知菱形ABCD的周长为16cm,∠ABC=60°,对角线AC和BD相交于点O,求AC和BD的长.
如图,已知菱形ABCD的周长为16cm,∠ABC=60°,对角线AC和BD相交于点O,求AC和BD的长.
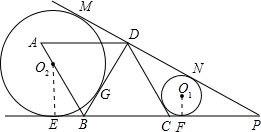 上,半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N,半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G.
上,半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N,半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G.