题目内容
【题目】如图,有一个水池,其底面是边长为16尺的正方形,一根芦苇AB生长在它的正中央,高出水面部分BC的长为2尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B′,则这根芦苇AB的长是( )
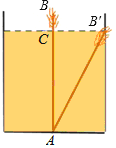
A. 15尺B. 16尺C. 17尺D. 18尺
【答案】C
【解析】
我们可以将其转化为数学几何图形,如图所示,根据题意,可知EB'的长为16尺,则B'C=8尺,设出AB=AB'=x尺,表示出水深AC,根据勾股定理建立方程,求出的方程的解即可得到芦苇的长.
解:依题意画出图形,
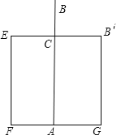
设芦苇长AB=AB′=x尺,则水深AC=(x-2)尺,
因为B'E=16尺,所以B'C=8尺
在Rt△AB'C中,82+(x-2)2=x2,
解之得:x=17,
即芦苇长17尺.
故选:C.

练习册系列答案
相关题目