题目内容
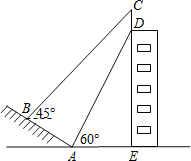
【题目】如图,山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.在高楼的顶端竖立一块倒计时牌CD,在点B处测量计时牌的顶端C的仰角是45°,在点A处测量计时牌的底端D的仰角是60°,求这块倒计时牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:
,AB=10米,AE=15米.在高楼的顶端竖立一块倒计时牌CD,在点B处测量计时牌的顶端C的仰角是45°,在点A处测量计时牌的底端D的仰角是60°,求这块倒计时牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
【答案】2.7m.
【解析】
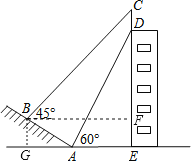
试题分析: 首先作BF⊥DE于点F,BG⊥AE于点G,得出四边形BGEF为矩形,进而求出CF,EF,DE的长,进而得出答案.
试题解析:作BF⊥DE于点F,BG⊥AE于点G,
∵CE⊥AE,
∴四边形BGEF为矩形,
∴BG=EF,BF=GE,
在Rt△ADE中,
∵tan∠ADE=![]() ,
,
∴DE=AEtan∠ADE=15![]() ,
,
∵山坡AB的坡度i=1:![]() ,AB=10,
,AB=10,
∴BG=5,AG=5![]() ,
,
∴EF=BG=5,BF=AG+AE=5![]() +15,
+15,
∵∠CBF=45°
∴CF=BF=5![]() +15,
+15,
∴CD=CF+EF-DE=20-10![]() ≈20-10×1.732=2.68≈2.7(m),
≈20-10×1.732=2.68≈2.7(m),
答:这块宣传牌CD的高度为2.7米.

练习册系列答案
相关题目