题目内容
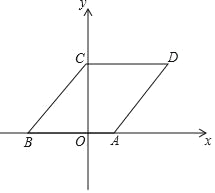
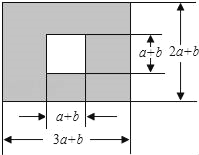
【题目】如图，某市有一块长为(3a+b)米、宽为(2a+b)米的长方形地块，中间是边长为(a+b)米的正方形，规划部门计划将在中间的正方形修建一座雕像，四周的阴影部分进行绿化．
(1)绿化的面积是多少平方米？(用含字母a、b的式子表示)
(2)求出当a＝10，b＝12时的绿化面积．
【答案】(1)绿化面积是(5a2+3ab)平方米；(2)绿化面积是860平方米．
【解析】
（1）根据长方形面积减去正方形面积表示出阴影部分面积，即为绿化面积；
（2）将a＝10，b＝12代入化简后的式子中计算即可得到结果．
(1)依题意得：
(3a+b)(2a+b)﹣(a+b)2
＝6a2+3ab+2ab+b2﹣a2﹣2ab﹣b2
＝(5a2+3ab)平方米．
答：绿化面积是(5a2+3ab)平方米；
(2)当a＝10，b＝12时，原式＝500+360＝860(平方米)．
答：绿化面积是860平方米．
练习册系列答案
寒假大串联黄山书社系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
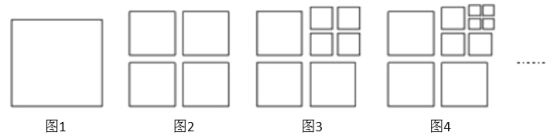
【题目】将图1中的正方形剪开得到图2，则图2中共有4个正方形；将图2中的一个正方形剪开得到图3，图3中共有7个正方形；将图3中4个较小的正方中的一个剪开得到图4，则图4中共有10个正方形，照这个规律剪下去……
（1）根据图中的规律补全下表：
图形标号 | 1 | 2 | 3 | 4 | 5 | 6 |
| n |
正方形个数 | 1 | 4 | 7 | 10 |
|
（2）求第几幅图形中有2020个正方形？
