题目内容
二次函数 的最小值是
的最小值是
 的最小值是
的最小值是A. | B.1 | C.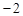 | D.2 |
D
试题分析:∵(x-1)2>O∴(x-1)2+2≥2 ∴当x=1时,y有最小值,y=2
点评:要求学生熟练的掌握二次函数的三种表达式,有一般式,两点式,顶点式。属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
 的最小值是
的最小值是A. | B.1 | C.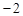 | D.2 |

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案