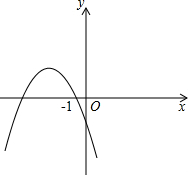题目内容

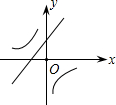
二次函数y=ax2+bx+c的图象如图所示．下列结论正确的是（　　）
A．3|a|+|c|＞2|b|B．3|a|+|c|=2|b|C．3|a|+|c|＜2|b|D．3|a|+|c|≤2|b|

由函数图象可知a＜0，c＜0，由对称轴x=-
b
2a
＞0，可知b＞0，
∴3|a|+|c|-2|b|=-（3a+2b+c），
∵当x=1时，y=a+b+c＞0，①
又对称轴x=-
b
2a
＞1，解得2a+b＞0，②
①+②得3a+2b+c＞0，
∴-（3a+2b+c）＜0，
∴3|a|+|c|＜2|b|．
故选C．
练习册系列答案
相关题目
如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（-3，0），对称轴为x=-1．给出四个结论：①b2＞4ac；②2a+b=0；③a-b+c=0；④5a＜b．其中正确的有（　　）
A．1个B．2个C．3个D．4个
（1）在同一直角坐标系中画抛物线y=x2-2x-3与双曲线y=
2
x
；
（2）观察图形，方程组的解的近似值为______．
如图，函数y=ax2-bx+c的图象过点（-1，0），则
a
b+c
+
b
c+a
+
c
a+b
的值为______．
如图，在平面直角坐标系中，抛物线y=
1
2
x2经过平移得到抛物线y=
1
2
x2-2x，其对称轴与两段抛物线所围成的阴影部分的面积为（　　）
A．2B．4C．8D．16
如图，二次函数y=ax2+bx+c（a≠0）的图象经过点（1，2）且与x轴交点的横坐标分别为x1，x2，其中-1＜x1＜0，1＜x2＜2，下列结论：4a+2b+c＜0，2a+b＜0，b2+8a＞4ac，a＜-1，其中结论正确的有（　　）
A．1个B．2个C．3个D．4个
已知函数y=ax2+ax与函数y=
a
x
（a＜0），则它们在同一坐标系中的大致图象是（　　）
A．B．C．D．
抛物线y=ax2+bx+c图象如图所示，则一次函数y=-bx-4ac+b2与反比例函数y=
a+b+c
x
在同一坐标系内的图象大致为（　　）
A．B．C．D．
已知点A（x1，y1）、B（x2，y2）在二次函数y=-（x-1）2+1的图象上，若-1＜x1＜0，3＜x2＜4，则y1______y2（填“＞”、“＜”或“=”）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网