题目内容
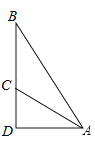
【题目】已知:如图,△ABC中,∠CAB=90°,AC=AB,点D、E是BC上的两点,且∠DAE=45°,△ADC与△ADF关于直线AD对称.
(1)求证:△AEF≌△AEB;
(2)∠DFE= °.

【答案】(1)证明见解析;(2)90°.
【解析】
试题本题考查了全等三角形的判定和性质,轴对称的性质,熟练掌握全等三角形的判定和性质是解题的关键.
(1)根据折叠的性质得到△AFD≌△ADC,根据全等三角形的性质得到AC=AF,CD=FD,∠C=∠DFA,∠CAD=∠FAD,由于AB=AC,于是得到AF=AB,证得∠FAE=∠BAE,即可得到结论;
(2)由(1)知△AFE≌△ABE,根据全等三角形的性质得到∠AFE=∠C,EF=EC,即可得到结论.
试题解析:解:(1)∵把△ADC沿着AD折叠,得到△ADF,
∴△AFD≌△ADC;
∴AC=AF,CD=FD,∠C=∠DFA,∠CAD=∠FAD,
∵AB=AC,
∴AF=AB,
∵∠DAE=45°,
∴∠FAE=∠BAE,
在△AFE与△ACE中,
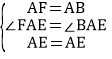 ,
,
∴△AFE≌△ABE;
(2)由(1)知△AFE≌△ABE,
∴∠AFE=∠C,EF=EC,
∴∠DFE=∠DFA+∠EFA=∠B+∠C=90°.
故答案为:90°.

练习册系列答案
相关题目