题目内容
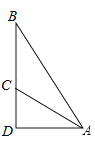
【题目】如图所示,在△ACB中,∠ACB=90゜,CD⊥AB于D.
(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于E、F , 求证:∠CEF=∠CFE.
【答案】
(1)
证明:∵∠ACB=90゜,CD⊥AB于D,
∴∠ACD+∠BCD=90°,∠B+∠BCD=90°,
∴∠ACD=∠B;
(2)
在Rt△AFC中,∠CFA=90°-∠CAF,
同理在Rt△AED中,∠AED=90°-∠DAE.
又∵AF平分∠CAB,
∴∠CAF=∠DAE,
∴∠AED=∠CFE,
又∵∠CEF=∠AED,
∴∠CEF=∠CFE.
【解析】(1)由于∠ACD与∠B都是∠BCD的余角,根据同角的余角相等即可得(2)根据直角三角形两锐角互余得出∠CFA=90°-∠CAF , ∠AED=90°-∠DAE , 再根据角平分线的定义得出∠CAF=∠DAE , 然后由对顶角相等的性质,等量代换即可证明∠CEF=∠CFE.
【考点精析】掌握解直角三角形是解答本题的根本,需要知道解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目