Question

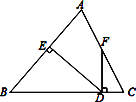
【题目】如图，AB为⊙O的直径，劣弧，BD∥CE，连接AE并延长交BD于D．

（1）求证：BD是⊙O的切线；

（2）若⊙O的半径为2cm，AC=3cm，求BD的长．

Answer 1

【答案】（1）证明见解析；（2）

【解析】

试题（1）根据题意得出AB平分CE，由垂径定理得推论得出AB⊥CE，再由BD∥CE，得出BD是⊙O的切线；
（2）连接BE，则∠AEB=90°，在直角三角形中，利用三角函数的定义求得AD，再在Rt△ABD中，由勾股定理得出BD的长．

试题解析：

（1）证明：

∵AB是直径，（1分）

∴AB⊥CE

∵BD∥CE，

∴DB⊥AB，

∴BD是⊙O的切线

（2）解：连接BE，∵AB为⊙O的直径（4分），

∴∠AEB=90°

∴在Rt△ABE中，cos∠BAE＝

∴在Rt△ABD中，cos∠BAD＝，

∴

∴在Rt△ABD中，由勾股定理得：BD＝．