题目内容
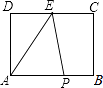
【题目】如图,四边形纸片ABCD中,∠A=70°,∠B=80°,将纸片折叠,使C,D落在AB边上的C′,D′处,折痕为MN,则∠AMD′+∠BNC′=( ).

A. 60° B. 70° C. 80° D. 90°
【答案】A
【解析】根据折叠的性质得到∠3=∠4,∠5=∠6,利用四边形的内角和为360°得到∠3+∠5+∠C+∠D=360°,∠A+∠B+∠C+∠D=360°,则∠3+∠5=∠A+∠B=70°+80°=150°,∠4+∠6=150°,由∠1+∠4+∠2+∠6+∠A+∠B=360°可得∠1+∠2=360°-150°×2=60°,然后把∠1=30°代入计算即可得到∠2的度数.
解:如图,
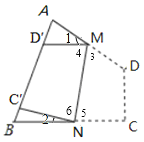
根据题意得∠3=∠4,∠5=∠6,
∵∠3+∠5+∠C+∠D=360°,
而∠A+∠B+∠C+∠D=360°,
∴∠3+∠5=∠A+∠B=70°+80°=150°,
∴∠4+∠6=150°,
∵∠1+∠4+∠2+∠6+∠A+∠B=360°,
∴∠1+∠2=360°-150°×2=60°,
即∠AMD′+∠BNC′=∠1+∠2=60°
故选A.
“点睛”本题考查了多边形的内角和定理:n边形的内角和为(n-2)180°.也考查了折叠的性质.

练习册系列答案
相关题目