题目内容
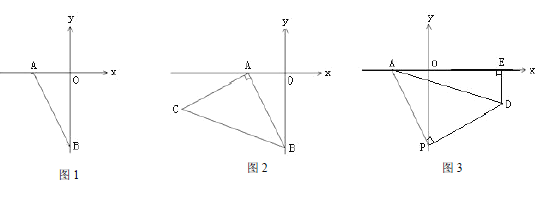
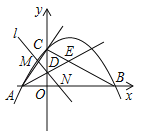
【题目】如图,在平面直角坐标系![]() 中,A、B为x轴上两点,C、D为y轴上的两点,经
中,A、B为x轴上两点,C、D为y轴上的两点,经
过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封
闭曲线称为“蛋线”.已知点C的坐标为(0,![]() ),点M是抛物线C2:
),点M是抛物线C2:![]() (
(![]() <0)的顶点.
<0)的顶点.

(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求![]() 的值.
的值.
【答案】解:(1)令y=0,则 ![]() ,
,
∵m<0,∴![]() ,解得:
,解得:![]() ,
, ![]() 。
。
∴A(![]() ,0)、B(3,0)。
,0)、B(3,0)。
(2)存在。理由如下:
∵设抛物线C1的表达式为![]() (
(![]() ),
),
把C(0,![]() )代入可得,
)代入可得,![]() 。
。
∴C1的表达式为:![]() ,即
,即![]() 。
。
设P(p,![]() ),
),
∴ S△PBC = S△POC + S△BOP –S△BOC =![]() 。
。
∵![]() <0,∴当
<0,∴当![]() 时,
时,![]() S△PBC最大值为
S△PBC最大值为![]() 。
。
(3)由C2可知: B(3,0),D(0,![]() ),M(1,
),M(1,![]() ),
),
∴BD2=![]() ,BM2=
,BM2=![]() ,DM2=
,DM2=![]() 。
。
∵∠MBD<90°, ∴讨论∠BMD=90°和∠BDM=90°两种情况:
当∠BMD=90°时,BM2+ DM2= BD2 ,即![]() +
+![]() =
=![]() ,
,
解得:![]() ,
, ![]() (舍去)。
(舍去)。
当∠BDM=90°时,BD2+ DM2= BM2 ,即![]() +
+![]() =
=![]() ,
,
解得:![]() ,
,![]() (舍去) 。
(舍去) 。
综上所述, ![]() 或
或![]() 时,△BDM为直角三角形。
时,△BDM为直角三角形。
【解析】(1)在![]() 中令y=0,即可得到A、B两点的坐标。
中令y=0,即可得到A、B两点的坐标。
(2)先用待定系数法得到抛物线C1的解析式,由S△PBC = S△POC + S△BOP –S△BOC得到△PBC面积的表达式,根据二次函数最值原理求出最大值。
(3)先表示出DM2,BD2,MB2,再分两种情况:①∠BMD=90°时;②∠BDM=90°时,讨论即可求得m的值。

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案【题目】某市现在有两种用电收费方法:
分时电表 | 普通电表 | |
峰时(8:00~21:00) | 谷时(21:00到次日8:00) | |
电价0.55元/千瓦·时 | 电价0.35元/千瓦·时 | 电价0.52元/千瓦·时 |
小明家所在的小区用的电表都换成了分时电表.
解决问题:
(1)小明家庭某月用电总量为![]() 千瓦·时(
千瓦·时(![]() 为常数);谷时用电
为常数);谷时用电![]() 千瓦·时,峰时用电
千瓦·时,峰时用电![]() 千瓦·时,分时计价时总价为
千瓦·时,分时计价时总价为![]() 元,普通计价时总价为
元,普通计价时总价为![]() 元,求
元,求![]() ,
,![]() 与用电量的函数关系式.
与用电量的函数关系式.
(2)小明家庭使用分时电表是不是一定比普通电表合算呢?
(3)下表是路皓家最近两个月用电的收据:
谷时用电(千瓦·时) | 峰时用电(千瓦·时) |
181 | 239 |
根据上表,请问用分时电表是否合算?