题目内容
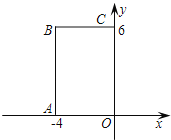
【题目】如图，在直角坐标系中，矩形OABC的顶点O在坐标原点，边OA在x轴上，OC在y轴上，如果矩形OA′B′C′与矩形OABC关于点O位似，且矩形OA′B′C′的面积等于矩形OABC面积的
，那么点B′的坐标是（ ）
A．（﹣2，3） B．（2，﹣3）
C．（3，﹣2）或（﹣2，3） D．（﹣2，3）或（2，﹣3）
【答案】D
【解析】
试题分析：由矩形OA′B′C′与矩形OABC关于点O位似，且矩形OA′B′C′的面积等于矩形OABC面积的
，利用相似三角形的面积比等于相似比的平方，即可求得矩形OA′B′C′与矩形OABC的位似比为1：2，又由点B的坐标为（﹣4，6），即可求得答案．
解：∵矩形OA′B′C′与矩形OABC关于点O位似，
∴矩形OA′B′C′∽矩形OABC，
∵矩形OA′B′C′的面积等于矩形OABC面积的，
∴位似比为：1：2，
∵点B的坐标为（﹣4，6），
∴点B′的坐标是：（﹣2，3）或（2，﹣3）．
故选：D．
练习册系列答案
快乐5加2金卷系列答案
相关题目
