题目内容
【题目】如图,四边形ABCD的对角线AC,BD交于点O,已知O是BD的中点,BE=DF,AF∥CE.
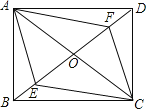
(1)求证:四边形AECF是平行四边形;
(2)若OA=OD,则四边形ABCD是什么特殊四边形?请证明你的结论.
【答案】(1)见解析(2)四边形ABCD为矩形
【解析】
试题分析:(1)根据平行线的性质推出∠AFO=∠CEO,∠FAO=∠ECO,求出OE=OF,证△AOF≌△COE,推出AF=CE,根据平行四边形的判定推出即可;
(2)根据全等得出OA=OC,求出AC=BD,再根据平行四边形和矩形的判定推出即可.
(1)证明:∵AF∥CE,
∴∠AFO=∠CEO,∠FAO=∠ECO,
∵O为BD的中点,即OB=OD,BE=DF,
∴OB﹣BE=OD﹣DF,即OE=OF,
在△AOF和△COE中

∴△AOF≌△COE(AAS),
∴AF=CE,
∵AF∥CE,
∴四边形AECF是平行四边形;
(2)若OA=OD,则四边形ABCD是矩形,
证明:∵△AOF≌△COE,
∴OA=OC,
∵OB=OD,
∴四边形ABCD是平行四边形.
∵OA=OD,∴OA=OB=OC=OD,即BD=AC,
∴四边形ABCD为矩形.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目