��Ŀ����
����Ŀ����֪������C1��y=ax2+bx�� ![]() ��a��0��������A��1��0����B����3��0����
��a��0��������A��1��0����B����3��0����
��1����������C1�Ľ���ʽ����д���䶥��C�����꣮
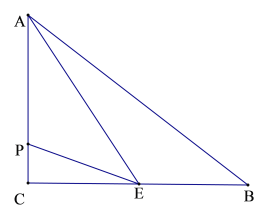
��2����ͼ1����������C1����ֱ��AC����ƽ�Ƶ�ij��ʱ�õ�������C2 �� ��ʱ��A��C�ֱ�ƽ�Ƶ���D��E�������F��������C1������x����Ϸ�������DEF����EFΪ�ĵ���ֱ�������Σ����F�����꣮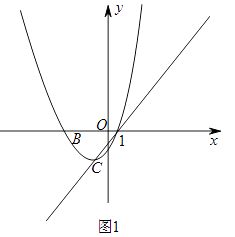
��3����ͼ2���ڣ�2���������£����M���߶�BC��һ���㣬EN��EM��ֱ��BF�ڵ�N����PΪ�߶�MN���е㣬����M�ӵ�B���C�˶�ʱ����tan��ENM��ֵ��α仯����˵�����ɣ��ڵ�M�����Cʱ��ֱ��д����P������·�߳���
���𰸡�
��1���⣺��������C1��y=ax2+bx�� ![]() ��a��0��������A��1��0����B����3��0����
��a��0��������A��1��0����B����3��0����
��  ���
��� ![]() ��
��
��������C1�Ľ���ʽΪy= ![]() x2+x��
x2+x�� ![]() ��
��
��y= ![]() x2+x��
x2+x�� ![]() =
= ![]() ��x+1��2��2��
��x+1��2��2��
�ඥ��C������Ϊ����1����2����
��2���⣺��ͼ1����CH��x����H��

��A��1��0����C����1����2����
��AH=CH=2��
���CAB=��ACH=45�㣬
��ֱ��AC�Ľ���ʽΪy=x��1��
�ߡ�DEF����EFΪ�ĵ���ֱ�������Σ�
���DEF=45�㣬
���DEF=��ACH��
��EF��y�ᣬ
��DE=AC=2 ![]() ��
��
��EF=4��
��F��m�� ![]() m2+m��
m2+m�� ![]() ������E��m��m��1����
������E��m��m��1����
�ࣨ�� ![]() m2+m��
m2+m�� ![]() ������m��1��=4��
������m��1��=4��
���m=��3���ᣩ��m=3��
��F��3��6����
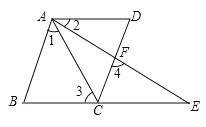
��3���⣺��tan��ENM��ֵΪ��ֵ���������仯��
��ͼ2�У���EG��AC����BF��G��

��DF��AC��BC��AC��
��DF��BC��
��DF=BC=AC��
���ı���DFBC��ƽ���ı��Σ�
�ߡ�CDF=90�㣬
���ı���DFBC�Ǿ��Σ�
��EG=BC=AC=2 ![]() ��
��
��EN��EM��
���MEN=90�㣬
�ߡ�CEG=90�㣬
���CEM=��NEG��
���ENG�ס�EMC��
�� ![]() =
= ![]() ��
��
��F��3��6����EF=4��
��E��3��2����
��C����1����2����
��EC=4 ![]() ��
��
�� ![]() =
= ![]() =2��
=2��
��tan��ENM= ![]() =2��
=2��
��tan��ENM��ֵΪ��ֵ���������仯��
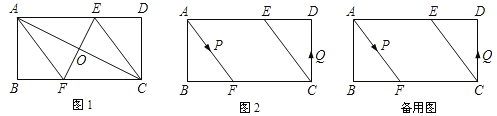
����ͼ3��1�У�

��ֱ��������EMN�У�PE= ![]() MN��ֱ��������BMN�У�PB=
MN��ֱ��������BMN�У�PB= ![]() MN��
MN��
��PE=PB��
���P��EB�Ĵ�ֱƽ�����ϣ�
���P������·�����߶�PP�䣬��ͼ3��2��

����M��B�غ�ʱ��
�ߡ�EGN�ס�ECB��
�� ![]() =
= ![]() ��
��
��EC=4 ![]() ��EG=BC=2
��EG=BC=2 ![]() ��
��
��EB=2 ![]() ��
��
�� ![]() =
= ![]() ��
��
��EN= ![]() ��
��
��P1P2�ǡ�BEN����λ�ߣ�
��P1P2= ![]() EN=
EN= ![]() ��
��
���M�����Cʱ����P������·�߳�Ϊ ![]() ��
��
����������1���ô���ϵ����������ý���ʽ���ѽ���ʽ��Ϊ����ʽ������ö������ꣻ��2������A��C����������ֱ��AC�Ľ���ʽΪy=x��1�����������EF=4�����EF��y�ᣬ��F��m�� ![]() m2+m��
m2+m�� ![]() ������E��m��m��1�����Ӷ��ó�����
������E��m��m��1�����Ӷ��ó����� ![]() m2+m��
m2+m�� ![]() ������m��1��=4���ⷽ�̼������F�����ꣻ��3��������ı���DFBC��ƽ�о��Σ���EG��AC����BF��G��Ȼ���жϳ���ENG�ס�EMC���������������ε����ʶ�Ӧ�߳ɱ����������tan��ENM��ֵ��������֤����P��EB�Ĵ�ֱƽ�����ϣ��Ƴ���P������·�����߶�PP������M��B�غ�ʱ�����ݹ��ɶ������������������EN��Ȼ�������������λ�߶���������á�
������m��1��=4���ⷽ�̼������F�����ꣻ��3��������ı���DFBC��ƽ�о��Σ���EG��AC����BF��G��Ȼ���жϳ���ENG�ס�EMC���������������ε����ʶ�Ӧ�߳ɱ����������tan��ENM��ֵ��������֤����P��EB�Ĵ�ֱƽ�����ϣ��Ƴ���P������·�����߶�PP������M��B�غ�ʱ�����ݹ��ɶ������������������EN��Ȼ�������������λ�߶���������á�

 ѧϰʵ����ϵ�д�
ѧϰʵ����ϵ�д�