题目内容
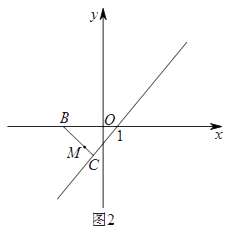
【题目】如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发以每秒2cm的速度沿A→C→B运动,设点P运动的时间是t秒,那么当t=____,△APE的面积等于6.

【答案】![]() 或5或9.
或5或9.
【解析】
分点P在线段AC上和点P在线段CE上和点P在线段EB上三种情况考虑,根据三角形的面积公式分别列出关于t的一元一次方程,解之即可得出结论.
解:∵BC=8cm,点E是BC的中点,
∴CE=![]() BC=4cm,
BC=4cm,
当点P在线段AC上,如图1所示,AP=2t,
∵∠C=90°,
∴S△APE=![]() APCE=
APCE=![]() = 4t=6,
= 4t=6,
解得:t=![]() ;
;
当点P在线段CE上,如图2所示,AC=6cm,PE=4-(t-3)=7-t,
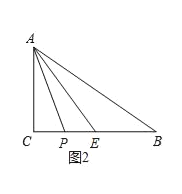
∴S△APE=![]() PE AC=
PE AC=![]() =6,
=6,
解得:t=5.
如图3,当P在线段BE上时, PE=t-3-4=t-7,
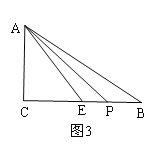
∴S△APE=![]() PE AC=
PE AC=![]() =6,
=6,
解得:t=9,
综上所述,t的值为![]() 或5或9;
或5或9;
故答案为: ![]() 或5或9.
或5或9.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
【题目】某商场销售国外、国内两种品牌的智能手机,这两种手机的进价和售价如下表所示:
国外品牌 | 国内品牌 | |
进价(元/部) | 4400 | 2000 |
售价(元/部) | 5000 | 2500 |
该商场计划购进两种手机若干部,共需14.8万元,预计全部销售后可毛获利润共2.7万元.[毛利润=(售价﹣进价)×销售量]
(1)该商场计划购进国外品牌、国内品牌两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少国外品牌手机的购进数量,增加国内品牌手机的购进数量.已知国内品牌手机增加的数量是国外品牌手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过15.6万元,该商场应该怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.