题目内容
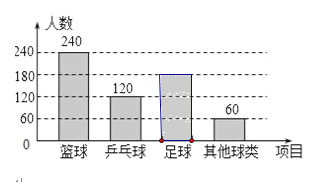
【题目】某学生社团为了解本校学生喜欢球类运动的情况,随机抽取了若干名学生进行问卷调查,要求每位学生只能填写一种自己喜欢的球类运动,并将调查的结果绘制成如下的两幅不完整的统计图.
请根据统计图表提供的信息,解答下列问题:

(1)参加调查的人数共有 人;在扇形图中,m= ;将条形图补充完整;
(2)如果该校有3500名学生,则估计喜欢“篮球”的学生共有多少人?
(3)该社团计划从篮球、足球和乒乓球中,随机抽取两种球类组织比赛,请用树状图或列表法,求抽取到的两种球类恰好是“篮球”和“足球”的概率.
【答案】(1)600 30,条形统计图见解析;(2)1400; (3)恰是篮球和足球的概率是![]() .
.
【解析】
试题分析:(1)用喜欢篮球的人数除以40%可得参加调查的人数,用1减去喜欢篮球、乒乓球、其他球类的百分比,可求得m值;(3)通过列表可求得恰是篮球和足球的概率是![]() .
.
试题解析:(1)∵240÷40%=600(人),∴参加调查的人数共有600人;∵1﹣40%﹣20%﹣10%=30%,
∴m=30.
(2)3500×40%=1400(人)答:喜欢“篮球”的学生共有1400人.
(3)
篮球 | 足球 | 乒乓球 | |
篮球 | 篮球、足球 | 篮球、乒乓球 | |
足球 | 足球、篮球 | / | 足球、乒乓球 |
乒乓球 | 乒乓球、篮球 | 乒乓球、足球 | / |
2÷6=![]() ,答:抽取到的两种球类恰好是“篮球”和“足球”的概率是
,答:抽取到的两种球类恰好是“篮球”和“足球”的概率是![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
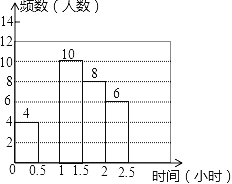
小学生10分钟应用题系列答案【题目】我市某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成家庭作业的时间不超过1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出如图所示的频数分布表和频数分布直方图的一部分.
时间/时 | 频数 | 百分比 |
0≤t<0.5 | 4 | 0.1 |
0.5≤t<1 | a | 0.3 |
1≤t<1.5 | 10 | 0.25 |
1.5≤t<2 | 8 | b |
2≤t<2.5 | 6 | 0.15 |
合计 | 1 |
(1)求表中a,b的值;
(2)补全频数分布直方图;
(3)请你估算该校1400名初中学生中,约有多少名学生在1.5小时以内完成了家庭作业.