��Ŀ����
����Ŀ��ƽ��ֱ������ϵ�У���A��B��C���㣬����AΪԭ�㣬��B�͵�C������ֱ�Ϊ��5,0���ͣ�1,2��.
��1��֤������ABCΪRT����
��2��������ֱ������ϵ����һ��D��ʹ����ABC����ABD���ƣ�д���������������ĵ�D�����꣬����ͬһ����ϵ�л������з���Ҫ��������Σ�
��3���ڵڣ�2����������ͼ�У�������������ֱ�������Σ�������ABC����ֱ�Ƕ�����ɵõ�һ���߶Σ��������������õ������߶�����ȡһ���߶Σ���ȡ������Ϊ���������߶εĸ���.
���𰸡���1��֤������������2��D1��1��-2����D2��4��-1����D3��4��1����D4��5��-10����D5��5��10����D6��5��-2.5����D7��5��2.5����D8��0��-10����D9��0��10����D10��0��-2.5����D11��0��2.5������ͼ����������3��p=![]() .
.
��������
���������������Ҫ�����˹��ɶ��������涨�������������ε����ʡ����ʹ�ʽ��֪ʶ�����÷������۵�˼���ǽ���ڣ�2��С��Ĺؼ���
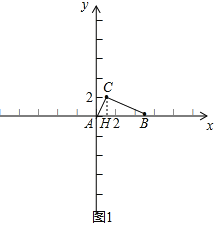
��1������C��CH��x����H����ͼ1��ֻ�����ù��ɶ������AB2��AC2��BC2��Ȼ�����ù��ɶ������涨���Ϳɽ�����⣻
��2����ABC���ABD���ƣ���Ӧ��ϵ��ȷ������������������������ABC�ס�ABD��������ABC�ס�BAD��������ABC�ס�ADB��������ABC�ס�DAB��������ABC�ס�BDA��������ABC�ס�DBA�����ۣ�Ȼ���������������ε����ʾͿɽ�����⣻
��3��ͼ�е�ֱ�������ε�ֱ�Ƕ�����A��B��C��D1��D2��D3��ֻ�����������ֱ�Ƕ�������߶ε������ͳ���Ϊ���������߶ε��������Ϳɽ�����⣮
�����������1������C��CH��x����H����ͼ1��
��A��0��0����B��5��0����C��1��2����
��AC=![]() ��BC=2
��BC=2![]() ��AB=5��
��AB=5��
��AB2=AC2+BC2��
���ABCΪRT����
 ��
��
��2��������ABC�ס�ABD������D1��1��-2����
������ABC�ס�BAD������D2��4��-1����D3��4��1����
������ABC�ס�ADB������D4��5��-10����D5��5��10����
������ABC�ס�DAB������D6��5��-2.5����D7��5��2.5����
������ABC�ס�BDA������D8��0��-10����D9��0��10����
������ABC�ס�DBA������D10��0��-2.5����D11��0��2.5����
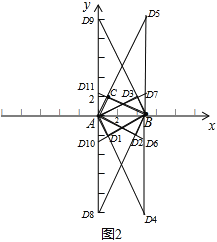
���з���Ҫ�����������ͼ2��ʾ��
 ��
��
��3��ͼ�е�ֱ�������ε�ֱ�Ƕ�����A��B��C��D1��D2��D3��
������ֱ�Ƕ�������߶ι���6��52=15����
����AB=5��CD1=D2D3=4��CD2=D1D3=5��CD3=D1D2=3��
�ʳ���Ϊ���������߶ι�7��������Ϊ���������߶ι�8����
��ȡ������Ϊ���������߶εĸ���Ϊp=![]() ��
��