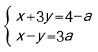题目内容
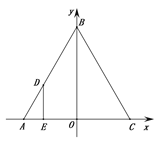
【题目】如图,等边△ABC的边AC在x轴上,AC中点O为坐标原点,已知C(2,0),动点D从A出发沿线段AB向终点B运动,速度为2个单位长度/秒,运动时间为t,过点D作DE⊥AC,垂足为E.
(1)当OD⊥AB时,求E点坐标.
(2)过E做EF⊥BC,垂足为F,过F作FG⊥AB,垂足为G,请用含t的式子表示线段DG的长度.
(3)在(2)的条件下,作点C关于EF的对称点H,连接HG并延长交直线DE于点Q,当t为何值时,HQ=EQ,并求出此时DG的长度.
【答案】(1)E点坐标为(![]() ,0);
,0);
(2)DG的长度为![]() 或
或![]()
(3)当t为![]() 时,HQ=EQ,并求出此时DG的长度是2.
时,HQ=EQ,并求出此时DG的长度是2.
【解析】试题分析:
(1)OD⊥AB时,∠A=60°,OA=2,∴OD=OAsin60°=![]() ,
,
在Rt△ODE中,∠DOE=30°,∴OE= ODcos30°=![]() ,
,
∴E(![]() )
)
(2)
如图:

AD=2t,则AE=t,EC=4-t,CF=2- ![]() ,BF=2+
,BF=2+ ![]() ,BG=1+
,BG=1+ ![]() ,
,
当D、 G重合时,
AD+BG=4,即2t+1+ ![]() =4,t=
=4,t=![]() ;,
;,
①当![]() 时,
时,
DG= AD+BG-4=2t+1+ ![]() -4=
-4=![]() ;
;
②当![]() 时,
时,
DG=4- (AD+BG)=4-(2t+1+ ![]() )=
)=![]() ;
;
(3)
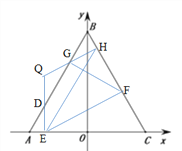
∵△ECH是等边三角形,∠HEC=60°,
∴∠QEH=30°,
∵QE=QH,
∴∠QHE=30°,
∴∠QHF=90°,
∴∠QHB=90°,
∵∠GBH=60°,
∴∠BGH=30°,
由对称可知BH=t,
在Rt△GBH中,BG=1+ ![]() ,∠BGH=30°,
,∠BGH=30°,
∴BG=2BH,即2t=1+ ,
∴t=![]() ,DG=
,DG=![]() =
=![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目