题目内容
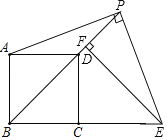
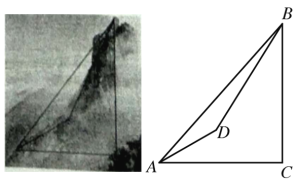
【题目】某学校数学兴趣小组想利用数学知识测量某座山的海拔高度，如图，他们在山腰A处测得山顶B的仰角为45°，他们从A处沿着坡度为i=1 : 
的斜坡前进1000 m到达D处，在D处测得山顶B的仰角为58°，若点A处的海拔为12米，求该座山顶点B处的海拔高度，(结果保留整数，参考数据:tan 58°≈1.60，sin 58°≈0. 85，cos 58°≈0.53，≈1. 732)
【答案】1488米.
【解析】
过D作DE⊥BC于点E，作DF⊥AC于点F，易知四边形DECF为矩形，在Rt△ADF中，利用三角函数可求出DF和AF，设BE=x米，在Rt△BDE中，利用三角函数可表示出DE的长度，再根据AC=BC建立方程求出x的值，最后用BC加上A点的海拔高度即为B处的海拔高度.
解：如图，过D作DE⊥BC于点E，作DF⊥AC于点F，
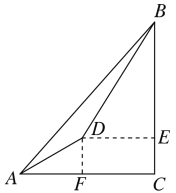
∵DE⊥BC，DF⊥AC，∠C=90°
∴四边形DECF为矩形，
∴DE=FC，DF=EC
∵山坡AD的坡度为i=1 : 
，
∴∠DAF=30°，
∴
米，
米
设BE=x米，在Rt△BDE中，∠BDE=58°，
∴
米，
在Rt△ABC中，∠BAC=45°，
∴AC=BC
∴AF+FC=BE+EC，即
解得
∴BC=BE+EC=976+500=1476米
∵A处的海拔高度为12米，
∴B处的海拔高度为1476+12=1488米
答：该座山顶点B处的海拔高度为1488米.
练习册系列答案
相关题目
