题目内容
【题目】如图1,直线![]() 分别交x轴、y轴于A、B两点,点P是线段AB上的一动点,以P为圆心,r为半径画圆.
分别交x轴、y轴于A、B两点,点P是线段AB上的一动点,以P为圆心,r为半径画圆.
(1)若点P的横坐标为﹣3,当⊙P与x轴相切时,则半径r为 ,此时⊙P与y轴的位置关系是 .(直接写结果)
(2)若![]() ,当⊙P与坐标轴有且只有3个公共点时,求点P的坐标.
,当⊙P与坐标轴有且只有3个公共点时,求点P的坐标.
(3)如图2,当圆心P与A重合,![]() 时,设点C为⊙P上的一个动点,连接OC,将线段OC绕点O顺时针旋转90°,得到线段OD,连接AD,求AD长的最值并直接写出对应的点D的坐标.
时,设点C为⊙P上的一个动点,连接OC,将线段OC绕点O顺时针旋转90°,得到线段OD,连接AD,求AD长的最值并直接写出对应的点D的坐标.


【答案】(1)![]() ,相离,(2)P
,相离,(2)P![]() 或P
或P![]() ;(3)当点D在线段AB上时,AD最小值为
;(3)当点D在线段AB上时,AD最小值为![]() ,点D坐标为
,点D坐标为![]() ,当点D在线段AB的延长线上时,AD最大值为
,当点D在线段AB的延长线上时,AD最大值为![]() ,点D坐标为
,点D坐标为![]()
【解析】
(1)根据坐标轴上点的坐标特征求出A点和B点的坐标,根据相似三角形的性质解答;
(2)根据直线与圆的位置关系解答;
(3)连接AC,BD,证明△AOC≌△BOD,求出BD的长,得到AD最长或最短距离,根据直角三角形的性质求出点D的坐标.
(1)当x=0时,y=4, 当y=0时,x=-4,
∴A点的坐标为(-4,0),B点的坐标为(0,4),
点N为⊙P与x轴的切点,连接PN,
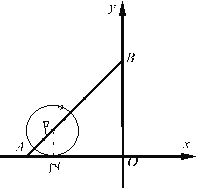
则PN∥OB,
∴![]() ,即
,即![]() ,
,
解得,PN=1,
x+4=1,
解得,x=3,
∵3>1,
∴⊙P与y轴的位置关系是相离,
故答案为:1;相离;
(2)当r=![]() ,⊙P与x轴相切时,
,⊙P与x轴相切时,
由![]() =x+4,得x=
=x+4,得x=![]() ,
,
则⊙P与y轴相交,
此时点P的坐标为(![]() ,
,![]() ),
),
当r=![]() ,⊙P与y轴相切时,
,⊙P与y轴相切时,
由y=![]() +4=
+4=![]() ,
,
则P与x轴相交,
此时点P的坐标为(-![]() ,
,![]() );
);
(3)连接AC、BD,

∵∠COD=∠AOB=90°
∴∠COA=∠DOB
易证△AOC≌△BOD
∴BD=AC=2
∴点D的运动轨迹是以点B为圆心,2为半径的圆,
当点D在线段AB上时,AD最小值为![]() ,点D坐标为
,点D坐标为![]() ;
;
当点D在线段AB的延长线上时,AD最大值为![]() ,点D坐标为
,点D坐标为![]() .
.

【题目】某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
选修课 | A | B | C | D | E | F |
人数 | 20 | 30 |
根据图标提供的信息,下列结论错误的是( )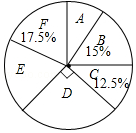
A.这次被调查的学生人数为200人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中最想选F的人数为35人
D.被调查的学生中最想选D的有55人