��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�����y=-x��ͼ��l�ǵڶ��������Ľ�ƽ���ߣ�
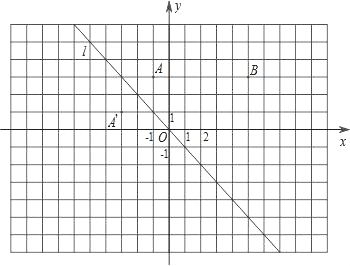
��1��ʵ����̽������ͼ�۲���֪A��-1��3������ֱ��l�ĶԳƵ�A�������Ϊ��-3��1��������д����B��5��3������ֱ��l�ĶԳƵ�B�������Ϊ ��
��2�������뷢�֣����ͼ�Σ��Լ�ѡ������һ�ԣ�ͨ���۲������꣬��ᷢ�֣�����ƽ������һ��P��m��n�����ڵڶ��������Ľ�ƽ����l�ĶԳƵ�P�������Ϊ ��
��3���������ع㣺
����֪����C��6��0����D��2��4��������ֱ��l��ȷ��һ��P��ʹ��P��C��D����ľ���֮����С����ͼ�л�����P��λ�ã�������ͼ�ۼ����������P�����꣮
�������������£������PC+PD����Сֵ��
���𰸡���1����-3��-5������2����-n��-m������3������ͼ��������P��1��-1������![]() .
.
��������
�����������1���۲�ͼ�εó���B��5��3������ֱ��l�ĶԳƵ�B������꼴�ɣ�
��2�������ܽ�õ�һ���Թ��ɣ�д��P��m��n�����ڵڶ��������Ľ�ƽ����l�ĶԳƵ�P������꼴�ɣ�
��3������ͼ������C����ֱ�� l �ĶԳƵ�C�䣬����C��D����l�ڵ�P������CP������ͼ��֪��PC=PC�䣬�����õ�PC+PD=C��D�������ʱP���꼴�ɣ������ù��ɶ������PC+PD����Сֵ���ɣ�
�����������1����������ã�B�䣨-3��-5����
��2����������ã�P�䣨-n��-m����
��3������ͼ������C����ֱ�� l �ĶԳƵ�C�䣬����C��D����l�ڵ�P������CP��
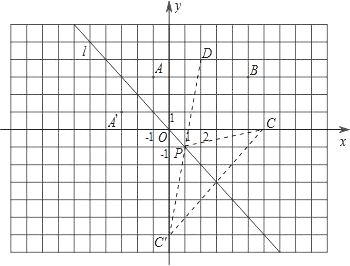
����ͼ��֪��PC=PC�䣬
��PC+PD=PC��+PD=C��D��
����P����
��C��6��0����
��C�䣨0��-6����
��ֱ��C��D�Ľ���ʽΪy=kx-6��
��D��2��4����
��k=5��
��ֱ��C��D�Ľ���ʽΪy=5x-6��
��![]() ��
��![]() ��
��
��P��1��-1����
��PC+PD=![]() ��
��

 ABC����ȫ�ž�ϵ�д�
ABC����ȫ�ž�ϵ�д�