[题目]如图.破残的圆形轮片上.弦AB的垂直平分线交弧AB于点C.交弦AB于点D．①求作此残片所在的圆O(不写作法.保留作图痕迹),②已知:AB=12cm.直径为20cm.求①中CD的长．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，破残的圆形轮片上，弦AB的垂直平分线交弧AB于点C，交弦AB于点D．

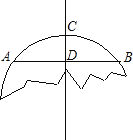
①求作此残片所在的圆O（不写作法，保留作图痕迹）；

②已知：AB=12cm，直径为20cm，求①中CD的长．

【答案】①见解析；②2cm．

【解析】

试题分析：①连接AC，作出弦AC的垂直平分线，与CD的交点即为圆心O，然后以点O为圆心，以OA为半径作圆即可；

②连接OB，根据垂径定理求出BD的长度，然后利用勾股定理求出OD的长度，从而不难得到CD的长．

解：①如图所示，⊙O即为所求作的圆；

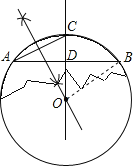
②连接OB，∵CD垂直平分AB，AB=12cm，

∴BD=AD=AB=6cm，

∵直径为20cm，

∴半径OB=OC=10cm，

在Rt△OBD中，OB2=BD2+OD2，

即102=62+OD2，

解得OD=8，

∴CD=10﹣8=2cm．

练习册系列答案

海淀黄冈名师导航系列答案

(1)、参照图象，求b、图②中c及d的值；

(2)、连接PQ，当PQ平分矩形ABCD的面积时，运动时间x的值为；

(3)、当两点改变速度后，设点P、Q在运动线路上相距的路程为y（cm），求y（cm）与运动时间x（秒）之间的函数关系式，并写出自变量x的取值范围；

(4)、若点P、点Q在运动路线上相距的路程为25cm，求x的值．

【题目】直角三角形有一条直角边为6，另两条边长是连续偶数，则该三角形周长为（）
A.20
B.22
C.24
D.26

A. 画∠A＝30° B. 您好！ C. 对顶角不等 D. 谁？

（1）求证：BE=CN

（2）试判断BM+CN与MN的大小关系，并说明理由.

（1）实验与探究：由图观察易知A（-1，3）关于直线l的对称点A′的坐标为（-3，1），请你写出点B（5，3）关于直线l的对称点B′的坐标为；

（2）归纳与发现：结合图形，自己选点再试一试，通过观察点的坐标，你会发现：坐标平面内任一点P（m，n）关于第二、四象限的角平分线l的对称点P′的坐标为；

（3）运用与拓广：

①已知两点C（6，0），D（2，4），试在直线l上确定一点P，使点P到C，D两点的距离之和最小，在图中画出点P的位置，保留作图痕迹，并求出点P的坐标．

②在①的条件下，试求出PC+PD的最小值．

【题目】如果收入15元记作+15元，那么支出20元记作（）元．
A.+5
B.+20
C.﹣5
D.﹣20

试题分类