题目内容
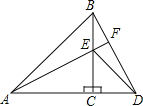
【题目】如图,直线MN经过正方形ABCD的顶点D且不与正方形的任何一边相交,AM⊥MN于M,CN⊥MN于N,BR⊥MN于R。

(1)求证:△ADM≌△DCN
(2)求证:MN=AM+CN
(3)试猜想BR与MN的数量关系,并证明你的猜想
【答案】(1)证明见解析;(2)证明见解析;(3)BR=MN;证明见解析.
【解析】
(1)要证△ADM≌△DCN,由于它们都是直角三角形,所以首先有直角相等,又由ABCD是正方形有AD=DC,再找一个条件即可,而由图形很容易分析得出∠ADM=∠DCN;
(2)由△AMD≌△DNC得到AM=DN,MD=NC,通过等量代换等到结论;
(3)作AE⊥BR于E,根据题意证明△ABE≌△DCN,然后再结合△ADM≌△DCN得到△ABE≌△ADM,细致证明通过等量代换等到结论即可.
证明:(1)∵AM⊥MN于点M,CN⊥MN于点N(已知),
∴∠AMD=∠DNC=90°(垂直的定义).
∴∠MAD+∠MDA=180°-90°=90°(三角形内角和定理).
∵四边形ABCD是正方形(已知),
∴∠ADC=90°,AD=DC.
∴∠MDA+∠NDC=180°-90°=90°(平角的定义).
∴∠MAD+∠MDA=∠NDC+∠NCD.
∴∠MAD=∠NDC.
在△AMB和△DNC中,
∵∠AMD=∠DNC,∠MAD=∠NDC,AD=DC,
∴△AMD≌△DNC(AAS).
(2)由(1)△AMD≌△DNC,
∴AM=DN,MD=NC.(全等三角形对应边相等)
∴MD+DN=AM+CN.
即MN=AM+CN.
(3)猜想BR=MN.
证明如下:
作AE⊥BR于E.
∵BR⊥MN,CN⊥MN(已知)
∴BR∥CN(垂直于同一直线的两条直线平行)
∴∠1=∠2(两直线平行同位角相等)
又四边形ABCD是正方形
∴AB⊥BC,DC⊥BC,
∴∠ABE=∠DCN=90°-∠1,
在△ABE和△DCN中,AB=DC,∠ABE=∠DCN,∠AEB=∠DNC=90°
∴△ABE≌△DCN(AAS)
由(1)△ADM≌△DCN
∴△ABE≌△ADM
∴AM=AE(全等三角形对应边相等).
又AE∥MR,AM∥ER,
∴四边形AERM是平行四边形
∴BR=BE+ER=CN+AM=DM+DN=MN.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案【题目】从边长为a的大正方形纸板中挖去一个边长为b的小正方形后,将其裁成四个相同的等腰梯形(如图1),然后拼成一个平行四边形(如图2)。那么通过计算两个图形的阴影部分的面积,可以验证成立的公式是( )
A.a2-b2=(a-b)2 | B.(a+b)2="a+2ab+b" |
C.(a-b)2=a2-2ab+b2 | D.a2-b2=(a-b)(a+b) |