题目内容
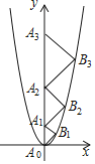
【题目】二次函数
的图象如图，点
位于坐标原点，点
，
，
，…，
在
轴的正半轴上，点
，
，
，…，
在二次函数位于第一象限的图象上，
，
，
，…，
都是直角顶点在抛物线上的等腰直角三角形，则的斜边长为________．
【答案】4040
【解析】
如图所示，过点B1，B2，B3分别作y轴的垂线，垂足分别为C，D，E，分别写出直线A0B1、直线A1B2、直线A2B3的解析式，将它们分别与y=x2联立，求得点B1，B2，B3的坐标，从而可得A0A1=2，A1A2=4，A2A3=6，发现规律后，按照规律即可求得
的斜边长．
解：如图所示，过点B1，B2，B3分别作y轴的垂线，垂足分别为C，D，E
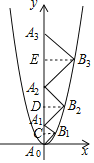
∵△A0B1A1，△A1B2A2，△A2B3A3…△A9B10A10都是直角顶点在抛物线上的等腰直角三角形
∴∠B1A0A1=∠B2A1A2=∠B3A2A3=45°
∴A0B1所在直线的解析式为：y=x
由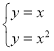
，得B1（1，1）
∴A0A1=2B1C=2
∴A1（0，2）
∴直线A1B2为：y=x+2
由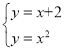
，得B2（2，4）
∴A1A2=2B2D=4
∴A2（0，6）
∴直线A2B3为：y=x+6
由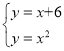
，得B3（3，9）
∴A2A3=2B3E=6
…
由上面A0A1=2，A1A2=4，A2A3=6，可以看出这些直角顶点在抛物线上的等腰直角三角形的斜边长依次加2
∴的斜边长为2+2019×2=4040
故答案为：4040．
练习册系列答案
阅读快车系列答案
相关题目
