Question

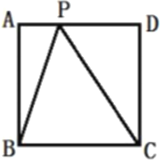
【题目】如图，正方形的边长为，点在上，连接，则的最大值为________．

Answer 1

【答案】

【解析】

先证明当AP=DP=2时，有最大值，过点B作BE⊥PC于点E，根据勾股定理求出PB=PC=，根据三角形的面积法，求出BE的值，进而即可得到答案．

设∠APB=x，∠DPC=y，

∴∠BPC=180°-∠APB -∠DPC=180°-（x+y），

∵当x＞0，y＞0时，，

∴，即：，当且仅当x=y时，，

∴当x=y时，x+y有最小值，此时，∠BPC=180°-（x+y）有最大值，即有最大值．

∵在正方形中，∠A=∠D，AB=CD，当∠APB=∠DPC时，

∴APB DPC（AAS），

∴AP=DP=2，

∴PB=PC=，

过点B作BE⊥PC于点E，

∵，

∴BE=，

∴=．

故答案是：．