Question

【题目】如图1，等边△ABC的边长为4cm，动点D从点B出发，沿射线BC方向移动，以AD为边作等边△ADE．

（1）在点D运动的过程中，点E能否移动至直线AB上？若能，求出此时BD的长；若不能，请说明理由；

（2）如图2，在点D从点B开始移动至点C的过程中，以等边△ADE的边AD、DE为边作ADEF．

①ADEF的面积是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由；

②若点M、N、P分别为AE、AD、DE上动点，直接写出MN+MP的最小值．

Answer 1

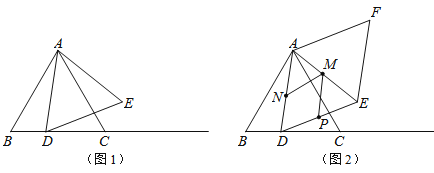
【答案】（1）不存在；（2）①存在，6；②3．

【解析】试题分析：（1）根据等边三角形的性质可知： 由三角形外角的性质可知从而可知： 所以点E不能移动到直线AB上.
（2）因为△ADE的面积所以当AD最短时，△ADE的面积有最小，根据垂线段最短可知当AD⊥BC时,△ADE的面积最小.四边形为平四边形，AE为对角线，所以平行四边形的面积是△ADE面积的2倍，所以△ADE的面积最小时，平行四边形的面积最小；
（3）当点N、M、P在一条直线上，且NP⊥AD时，MN+MP有最小值，最小值为AD与EF之间的距离．

试题解析：(1)不存在.

理由：如图1所示：

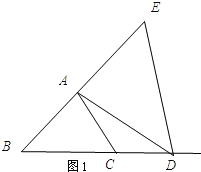
∵△ABC和△ADE均为等边三角形，

∴

∵

∴

又∵

∴

∴点E不能移动到直线AB上.

(2)①存在：在图(2)中，当AD⊥BC时,△ADE的面积最小.

在Rt△ADB中,

∴△ADE的面积

∵四边形ADEF为平四边形，AE为对角线，

∴平行四边形ADEF的面积是△ADE面积的2倍.

∴ADEF的面积的最小值

②如图3所示：作点P关于AE的对称点P1，

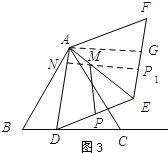
当点N、M、P在一条直线上，且NP⊥AD时，MN+MP有最小值，

过点A作AG∥NP1，

∵AN∥GP1,AG∥NP，

∴四边形ANP1G为平行四边形.

∴

即MN+MP的最小值为3.