题目内容
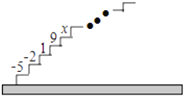
【题目】如图是二次函数y=![]() 图象的一部分.其对称轴为x=-1,且过点(-3,0).下列说法:(1)abc<0;(2)2a-b=0;(3)4a+2b+c=0;(4)若(-5,
图象的一部分.其对称轴为x=-1,且过点(-3,0).下列说法:(1)abc<0;(2)2a-b=0;(3)4a+2b+c=0;(4)若(-5,![]() ),
),![]() 是抛物线上两点,则
是抛物线上两点,则![]() >
>![]() .其中说法正确的是_____ (填序号)
.其中说法正确的是_____ (填序号)

【答案】(1)(2)(4)
【解析】分析:根据图象分别求出a、b、c的符号,即可判断(1),根据对称轴求出b=2a,代入2a-b即可判断(2),把x=2代入二次函数的解析式,再根据二次函数的性质即可判断(3),求出点(-5,y1)关于直线x=-1的对称点的坐标,根据对称轴判断y1和y2的大小,即可判断(4).
详解:∵二次函数的图象开口向上,
∴a>0,
∵二次函数的图象交y轴的负半轴于一点,
∴c<0,
∵对称轴是直线x=-1,
∴-![]() =-1,
=-1,
∴b=2a>0,
∴abc<0,
故(1)正确;
∵b=2a,
∴2a-b=0,
故(2)正确;
∵抛物线的对称轴为x=-1,且过点(-3,0),
∴抛物线与x轴另一交点为(1,0).
∵当x>-1时,y随x的增大而增大,
∴当x=2时y>0,即4a+2b+c>0,
故(3)错误;
∵(-5,y1)关于直线x=-1的对称点的坐标是(3,y1),
又∵当x>-1时,y随x的增大而增大,3>![]() ,
,
∴y1>y2,
故(4)正确;
故答案为(1)(2)(4).

【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |
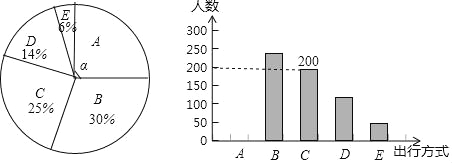
根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
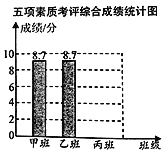
【题目】学校通过初评决定最后从甲、乙、丙三个班中推荐一个班为县级先进班集体,下表是三个班的五项素质考评得分表。
五项素质考评得分表(单位:分)
班级 | 行为规范 | 学习成绩 | 校运动会 | 艺术获奖 | 劳动卫生 |
甲班 | 10 | 10 | 6 | 10 | 7 |
乙班 | 10 | 8 | 8 | 9 | 8 |
丙班 | 9 | 10 | 9 | 6 | 9 |
根据统计表中的信息回答下列问题:
(1)请你补全五项成绩考评分析表中的数据:
班级 | 平均分 | 众数 | 中位数 |
甲班 | 8.6 | 10 | ③ |
乙班 | 8.6 | ② | 8 |
丙班 | ① | 9 | 9 |
(2)参照上表中的数据,你推荐哪个班为县级先进班集体?并说明理由。
(3)如果学校把行为规范、学习成绩、校运动会、艺术获奖、劳动卫生五项考评成绩按照3∶2∶1∶1∶3的比确定班级的综合成绩,学生处的李老师根据这个综合成绩,绘制了一幅不完整的条形统计图,请将这个统计图补充完整,按照这个成绩,应推荐哪个班为县级先进班集体?为什么?