Question

【题目】直线y= x﹣2与x、y轴分别交于点A、C．抛物线的图象经过A、C和点B（1，0）．
（1）求抛物线的解析式；
（2）在直线AC上方的抛物线上有一动点D，当D与直线AC的距离DE最大时，求出点D的坐标，并求出最大距离是多少？

Answer 1

【答案】
（1）

解：在直线解析式y= x﹣2中，令x=0，得y=﹣2；令y=0，得x=4，

∴A（4，0），C（0，﹣2）．

设抛物线的解析式为y=ax2+bx+c，

∵点A（4，0），B（1，0），C（0，﹣2）在抛物线上，

∴ ，

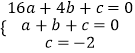解得a=- ，b= ，c=﹣2．

∴抛物线的解析式为：y= x2+ x﹣2．

（2）

解：设点D坐标为（x，y），则y= x2+ x﹣2．

在Rt△AOC中，OA=4，OC=2，由勾股定理得：AC= ．

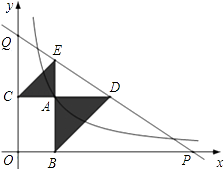
如答图1所示，连接CD、AD．

过点D作DF⊥y轴于点F，过点A作AG⊥FD交FD的延长线于点G，

则FD=x，DG=4﹣x，OF=AG=y，FC=y+2．

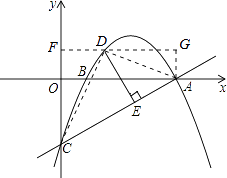
S△ACD=S梯形AGFC﹣S△CDF﹣S△ADG

= （AG+FC）FG﹣ FCFD﹣ DGAG

= （y+y+2）×4﹣ （y+2）x﹣ （4﹣x）y

=2y﹣x+4

将y= x2+ x﹣2代入得：S△ACD=2y﹣x+4=﹣x2+4x=﹣（x﹣2）2+4，

∴当x=2时，△ACD的面积最大，最大值为4．

当x=2时，y=1，∴D（2，1）．

∵S△ACD= ACDE，AC= ，

∴当△ACD的面积最大时，高DE最大，

则DE的最大值为： ．

∴当D与直线AC的距离DE最大时，点D的坐标为（2，1），最大距离为 ．

【解析】（1）首先求出点A，点C的坐标；然后利用待定系数法求出抛物线的解析式；（2）AC为定值，当DE最大时，△ACD的面积最大，因此只需要求出△ACD面积的最大值即可．如解答图所示，作辅助线，利用S△ACD=Sspan>梯形AGFC﹣S△CDF﹣S△ADG求出S△ACD的表达式，然后利用二次函数的性质求出最大值，并进而求出点D的坐标和DE的最大值．
【考点精析】通过灵活运用二次函数的图象和二次函数的性质，掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小即可以解答此题．