题目内容
【题目】如图,抛物线y=x2﹣4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q.
(1)这条抛物线的对称轴是 , 直线PQ与x轴所夹锐角的度数是;
(2)若两个三角形面积满足S△POQ= ![]() S△PAQ , 求m的值;
S△PAQ , 求m的值;
(3)当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求:①PD+DQ的最大值;②PDDQ的最大值.
【答案】
(1)2,45°
(2)解:如图

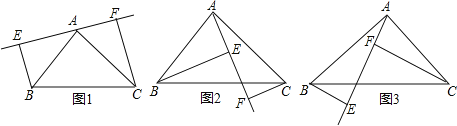
设直线PQ交x轴于点B,分别过O点,A点作PQ的垂线,垂足分别是E、F,显然当点B在OA的延长线时,S△POQ= ![]() S△PAQ不成立;
S△PAQ不成立;
①当点B落在线段OA上时,如图①,

![]() =
= ![]() =
= ![]() ,
,
由△OBE∽△ABF得, ![]() =
= ![]() =
= ![]() ,
,
∴AB=3OB,
∴OB= ![]() OA,
OA,
由y=x2﹣4x得点A(4,0),
∴OB=1,
∴B(1,0),
∴1+m=0,
∴m=﹣1;
②当点B落在线段AO的延长线上时,如图②,同理可得OB= ![]() OA=2,
OA=2,

∴B(﹣2,0),
∴﹣2+m=0,
∴m=2,
综上,当m=﹣1或2时,S△POQ= ![]() S△PAQ
S△PAQ
(3)解:①过点C作CH∥x轴交直线PQ于点H,如图③,可得△CHQ是等腰三角形,
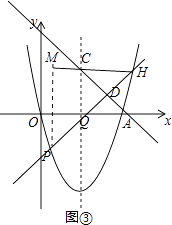
∵∠CDQ=45°+45°=90°,
∴AD⊥PH,
∴DQ=DH,
∴PD+DQ=PH,
过P点作PM⊥CH于点M,则△PMH是等腰直角三角形,
∴PH= ![]() PM,
PM,
∴当PM最大时,PH最大,
∴当点P在抛物线顶点处时,PM最大,此时PM=6,
∴PH的最大值为6 ![]() ,
,
即PD+DQ的最大值为6 ![]() .
.
②由①可知:PD+DQ≤6 ![]() ,
,
设PD=a,则DQ ![]() ﹣a,
﹣a,
∴PDDQ≤a(6 ![]() ﹣a)=﹣a2+6
﹣a)=﹣a2+6 ![]() a=﹣(a﹣3
a=﹣(a﹣3 ![]() )2+18,
)2+18,
∵当点P在抛物线的顶点时,a=3 ![]() ,
,
∴PDDQ≤18.
∴PDDQ的最大值为18.
方法二:
⑴略.
⑵过点A作x轴垂线,与直线PQ交于点D,设直线PQ与y轴交于点C,
∴C(0,m),D(4,4+m),
∵S△POQ= ![]() (Qx﹣Px)(QY﹣CY),
(Qx﹣Px)(QY﹣CY),
S△PAQ= ![]() (Qx﹣Px)(DY﹣AY),
(Qx﹣Px)(DY﹣AY),
∵ ![]() ,
,
∴ ![]() ,
,
∴m1=2,m2=﹣1.
⑶①设P(t,t2﹣4t)(0<t<4),
∵KPQ=1,∴lPQ:y=x+t2﹣5t,
∵C(2,2),A(4,0),
∴lAC:y=﹣x+4,
∴DX= ![]() ,DY=
,DY= ![]() ,
,
∴Q(2,t2﹣5t+2),
∵PQ⊥AC,垂足为点D,
∴点Q关于直线AC的对称点Q′(﹣t2+5t+2,2),
欲使PD+DQ取得最大值,只需PQ′有最大值,
PQ′= ![]() =
= ![]() ,
,
显然当t=2时,PQ′的最大值为6 ![]() ,
,
即PD+DQ的最大值为6 ![]() ,
,
②∵(PD+DQ)2≥4PDDQ,
∴PDDQ≤ ![]() =
= ![]() =18,
=18,
∴PDDQ的最大值为18.
【解析】方法一:
解:(1)∵y=x2﹣4x=(x﹣2)2﹣4,
∴抛物线的对称轴是x=2,
∵直线y=x+m,
∴直线与坐标轴的交点坐标为(﹣m,0),(0,m),
∴交点到原点的距离相等,
∴直线与坐标轴围成的三角形是等腰直角三角形,
∴直线PQ与x轴所夹锐角的度数是45°,
所以答案是x=2、45°.

 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案