题目内容
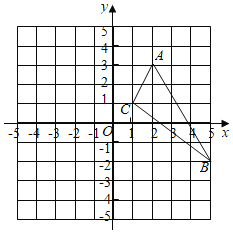
【题目】如图,在平面直角坐标系中,已知两点A(3,0),B(0,4),点C在第一象限,AB⊥BC,BC=BA,点P在线段OB上,OP=OA,AP的延长线与CB的延长线交于点M,AB与CP交于点N.

(1)点C的坐标为: ;
(2)求证:BM=BN;
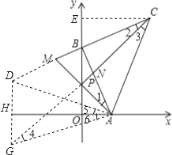
(3)设点C关于直线AB的对称点为D,点C关于直线AP的对称点为G,求证:D,G关于x轴对称.
【答案】(1)(4,7)(2)见解析(3)见解析
【解析】
(1)过点C作CE⊥y轴于点E,根据AAS证明△AOB≌△BEC,根据全等三角形的性质即可得到点C的坐标;
(2)根据全等三角形的性质和等量替换可得∠1=∠2,根据ASA证明△ABM≌△CBN,即可证得BM=BN;
(3)根据SAS证明△DAH≌△GAH,根据全等三角形的性质即可求解.
(1)过点C作CE⊥y轴于点E,故∠BEC=90°,
∴∠BEC=∠AOB,
∴∠ABC=90°,
∴∠ABO+∠CBE=90°,
∵∠ABO+∠BAO=90°
∴∠CBE=∠BAO
∴△AOB≌△BEC(AAS)
∴CE=OB=4,BE=OA=3,
∴OE=OB+BE=7,
∴C点坐标为(4,7)
(2)∵△AOB≌△BEC
∴BE=OA=OP,CE=BO,
∴PE=OB=CE,
∴∠EPC=45°,∠APC=90°,
∴∠1=∠2,
∴△ABM≌△CBN(ASA)
∴BM=BN,
(3)点C关于直线AB的对称点为D,点C关于直线AP的对称点为G,
∴AD=AC,AG=AC,
∴AD=AG,
∵∠1=∠5,∠1=∠6,
∴∠5=∠6,
在△DAH与△GAH中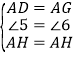
∴△DAH≌△GAH(SAS)
∴D,G关于x轴对称.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案【题目】某批发商计划将一批海产品由A地运往B地.汽车货运公司和铁路货运公司均开办海产品运输业务.已知运输路程为120千米,汽车和火车的速度分别为60千米/时、100千米/时.两货运公司的收费项目及收费标准如下表所示:
运输工具 | 运输费单价/ (元/吨·千米) | 冷藏费单价/ (元/吨·小时) | 过路费/元 | 装卸及管理费/元 |
汽 车 | 2 | 5 | 200 | 0 |
火 车 | 1.8 | 5 | 0 | 1600 |
注:“元/吨·千米”表示每吨货物每千米的运费;“元/吨·小时”表示每吨货物每小时的冷藏费.
(1)设该批发商待运的海产品有x(吨),汽车货运公司和铁路货运公司所要收取的费用分别为y1(元)和y2(元),试求y1、y2与x之间的函数关系式.
(2)若该批发商待运的海产品不少于30吨,为节省运费,他应选择哪个货运公司承担运输业务?
【题目】“十一”黄金周,坚胜家电城大力促销,收银情况一直看好![]() 下表为当天与前一天的营业额的涨跌情况
下表为当天与前一天的营业额的涨跌情况![]() 已知9月30日的营业额为26万元.
已知9月30日的营业额为26万元.
10月1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
4 | 3 | 2 | 0 |
|
|
|
![]() 黄金周内收入最低的哪一天?
黄金周内收入最低的哪一天?![]() 直接回答,不必写过程
直接回答,不必写过程![]() .
.
![]() 黄金周内平均每天的营业额是多少?
黄金周内平均每天的营业额是多少?