题目内容
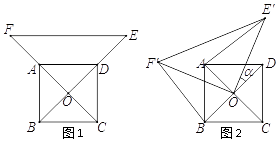
【题目】如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.
(1)请在图中画出平移后的△A′B′C′,
(2)再在图中画出△A′B′C′的高C′D′,并求出△ABC在整个平移过程中线段AC扫过的面积为________.
(3)能使S△MBC=S△ABC的格点M共有_______个(点M异于点A)

【答案】(1)见解析;(2)作图见解析;32;(3)4.
【解析】
(1)分别将点A、B、C向左平移2格,再向上平移4格,得到点A′、B′、C′,然后顺次连接;
(2)过点C′作C′D′⊥A′B′的延长线于点D′即可,利用分割法即可求出线段AC扫过的面积;
(3)利用平行线的性质过点A作出BC的平行线进而得出符合题意的点.
解:(1)如图所示:△A′B′C′即为所求;
(2)如图所示:C′D′即为所求;
线段AC扫过的面积为:![]() ,
,
故答案为:32;

(3)如图所示:能使S△MBC=S△ABC的格点M的个数有4个.
故答案为:4.


练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中,x与y的部分对应值如下表:
x | ﹣3 | ﹣2 | ﹣1 | 0 |
y | 0 | ﹣3 | ﹣4 | ﹣3 |
下列结论:
①ac<0;
②当x>1时,y随x的增大而增大;
③﹣4是方程ax2+(b﹣4)x+c=0的一个根;
④当﹣1<x<0时,ax2+(b﹣1)x+c+3>0.其中正确结论的个数为( )
A.4个
B.3个
C.2个
D.1个