题目内容
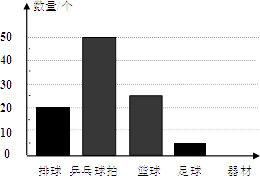
【题目】某市球类运动协会为了筹备一次大型体育活动,购进了一定数量的体育器材,器材管理员对购买的部分器材进行了统计,图表和图是器材管理员通过采集数据后,绘制的两幅不完整的频率分布表与频数分布直方图.请你根据图表中提供的信息,解答以下问题: 
频率分布表 | ||
器材种类 | 频数 | 频率 |
排 球 | 20 | |
乒乓球拍 | 50 | 0.50 |
篮 球 | 25 | 0.25 |
足 球 | ||
合 计 | 1 | |
(1)填充频率分布表中的空格.
(2)在图中,将表示“排球”和“足球”的部分补充完整.
(3)若该协会购买这批体育器材时,篮球和足球一共花去950元,且足球每个的价格比篮球多10元,现根据筹备实际需要,准备再采购篮球和足球这两种球共10个(两种球的个数都不能为0),计划资金不超过320元,试问该协会有哪几种购买方案?
【答案】
(1)解:50÷0.50=100个;
则足球有100﹣20﹣50﹣25=5个;
足球频率 ![]() =0.05;
=0.05;
排球频率 ![]() =0.2;
=0.2;
合计为100.
故答案为:0.2; 5,0.05; 100
(2)解:如图:
(3)解:设篮球每个x元,足球每个(x+10)元,列方程得,
25x+5(x+10)=950,
解得x=30,
则篮球每个30元,足球每个40元.
设再买y个篮球,列不等式得,
30y+40(10﹣y)≤320,
解得y≥8,
由于篮球足球共10个,
则篮球8个,足球2个;或篮球9个,足球1个
【解析】(1)根据乒乓球的总数为50,频数为0.50,求出体育器材总数,然后减去乒乓球、排球、篮球数目,即可得到足球频数、频率及合计数.(2)根据统计表中的数据,将统计图补充完整即可.(3)列方程求出篮球和足球的单价,再根据单价列出不等式,推知购买方案.
【考点精析】通过灵活运用一元一次不等式组的应用和频数分布直方图,掌握1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案;特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图)即可以解答此题.

