题目内容
【题目】如图，△ABC中，BA=BC，BD是三角形的角平分线，DE∥BC交AB于E，下列结论：①∠1=∠3；②
；③
。正确的有__________。（填序号）
【答案】①②③
【解析】
由角平分线可得∠1=∠2，再由DE∥BC得到内错角相等，可判断①；由等腰三角形三线合一可得D为AC的中点，所以DE为中位线，即可判断②；由△AED∽△ABC，且相似比为1:2，可得面积比，从而判断③.
∵BD平分∠ABC，
∴∠1=∠2
∵DE∥BC
∴∠3=∠2
∴∠1=∠3，①正确；
∵△ABC中，BA=BC，BD是三角形的角平分线
∴D为AC的中点，
又∵DE∥BC
∴DE为△ABC的中位线
∴
，故②正确；
∵DE∥BC
∴△AED∽△ABC
∴
∴
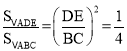
，故③正确；
所以正确的有①②③.
练习册系列答案
相关题目
